题目内容
已知椭圆E：
＝1(a＞b＞0)的左、右焦点分别为F1，F2，点P是x轴上方椭圆E上的一点，且PF1⊥F1F2，|PF1|＝
，|PF2|＝
．
(Ⅰ)求椭圆E的方程和P点的坐标；
(Ⅱ)判断以PF2为直径的圆与以椭圆E的长轴为直径的圆的位置关系；
(Ⅲ)若点G是椭圆C：
＝1(m＞n＞0)上的任意一点，F是椭圆C的一个焦点，探究以GF为直径的圆与以椭圆C的长轴为直径的圆的位置关系
答案：
解析：
解析：
|
解：(Ⅰ) 所以椭圆 (Ⅱ)线段 ∴以 圆 以椭圆 两圆圆心 ∴两圆心间的距离 |
在椭圆
上
，1分
，
2分
，
．
的方程是：
．4分
，
5分
的中点
的方程为
．8分
的长轴为直径的圆
的半径
，
、
分别是
和
的中点，
，所以两圆内切．14分
练习册系列答案
相关题目
＝1(a＞b＞o)的离心率e＝
，且经过点(
，1)，O为坐标原点．
：＋＝1(a＞b＞0)的长轴AB长为4，离心率e＝，O为坐标原点，过B的直线l与x轴垂直．P是椭圆上异于A、B的任意一点，PH⊥x轴，H为垂足，延长HP到点Q使得HP＝PQ，连结AQ延长交直线
于点M，N为
的中点．
为直径的圆
上；
：＋＝1(a＞b＞0)的长轴AB长为4，离心率e＝，O为坐标原点，过B的直线l与x轴垂直．P是椭圆上异于A、B的任意一点，PH⊥x轴，H为垂足，延长HP到点Q使得HP＝PQ，连结AQ延长交直线
于点M，N为
的中点．
（1）求椭圆
为直径的圆
上；
＝1(a>b>0)的长轴长是短轴长的2倍，且过点C(2,1)，点C关于原点O的对称点为D.
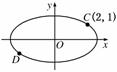(3)平行于CD的直线l交椭圆E于M、N两点，求△CMN面积的最大值，并求此时直线l的方程．