题目内容
已知F1、F2是双曲线
-
=1(a>0,b>0)的两个焦点,以线段F1F2为斜边作等腰直角三角形F1MF2,如果线段MF1的中点在双曲线上,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析:记双曲线的焦距为2C、依题意知点M在y轴上,不妨设F1、F2分别是双曲线的左、右焦点,M在y轴正半轴上,则可表示出F1和M的坐标,进而可表示出线段MF1的中点坐标代入双曲线方程,化简整理即可求得e.
解答:解:记双曲线的焦距为2C、依题意知点M在y轴上,
不妨设F1、F2分别是双曲线的左、右焦点,M在y轴正半轴上,则有F1(-c,0),M(0,c),
∴线段MF1的中点坐标是(-
,
).
又∵线段MF1的中点在双曲线上,
∴
-
=1,即
-
=4,
-
=4,(e2)2-6e2+4=0,e2=3±
.又e2>1,
∴e2=3
∵(
)2=3+
,
∴e=
.
故选C
不妨设F1、F2分别是双曲线的左、右焦点,M在y轴正半轴上,则有F1(-c,0),M(0,c),
∴线段MF1的中点坐标是(-
| c |
| 2 |
| c |
| 2 |
又∵线段MF1的中点在双曲线上,
∴
(-
| ||
| a2 |
(
| ||
| b2 |
| c2 |
| a2 |
| c2 |
| b2 |
| c2 |
| a2 |
| c2 |
| c2-a2 |
| 5 |
∴e2=3
| 5 |
∵(
| ||||
| 2 |
| 5 |
∴e=
| ||||
| 2 |
故选C
点评:本题主要考查了直线与双曲线的关系以及求离心率的问题.考查了学生的综合分析问题和基本的运算能力.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
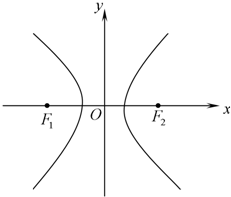
 的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.
的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.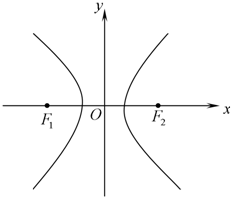
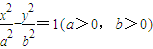 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若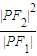 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )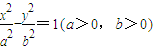 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若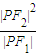 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )