题目内容
12.定义函数f(x)的导函数为f′(x),已知若f(x)=xk(k∈Z),则f′(x)=kxk-1,并且有如下运算律成立;(1)(f(x)+g(x))′=f′(x)+g′(x);
(2)(f(x)-g(x))′=f′(x)-g′(x);
(3)(f(x)•g(x))′=f(x)•g′(x)+f′(x)-g(x);
(4)($\frac{f(x)}{g(x)}$)′=$\frac{g(x)•f′(x)-f(x)•g′(x)}{(g(x))^{2}}$.
导函数在求函数最值时有很大的作用,已知函数在某个区间上的最大值和最小值必在区间的端点或使导函数为0的x处取到.请根据上述结论.回答下列问题:
(1)求下列函数的导函数:f1(x)=x3;f2(x)=x-2.
(2)求下列函数的导函数:g1(x)=x2(x-3);g2(x)=$\frac{x}{x+2}$.
(3)求函数f(x)=$\frac{1}{3}$x2-x-3当区间[-$\frac{3}{2}$,$\frac{3}{2}$]内取值时的最大值和最小值.
分析 (1)根据导数公式进行求解即可.
(2)根据导数公式进行求解即可.
(3)求函数f(x)=$\frac{1}{3}$x2-x-3的导数,判断函数的单调性即可.
解答 解:(1)∵f1(x)=x3;
∴f1′(x)=3x2;
∵f2(x)=x-2.
∴f2′(x)=-2x-3.
(2)∵g1(x)=x2(x-3)=x3-3x2;g2(x)=$\frac{x}{x+2}$=$\frac{x+2-2}{x+2}$=1-$\frac{2}{x+2}$.
∴g1′(x)=3x2-6x;g2′(x)=$\frac{2}{(x+2)^{2}}$.
(3)∵函数f(x)=$\frac{1}{3}$x2-x-3,
∴f′(x)=$\frac{2}{3}$x-1,
由f′(x)>0得x>$\frac{3}{2}$,此时函数递增,
由f′(x)<0得x<$\frac{3}{2}$,此时函数递减,
故当x∈[-$\frac{3}{2}$,$\frac{3}{2}$]时,函数单调递减,
此时函数的最小值为f($\frac{3}{2}$)=$\frac{1}{3}$•($\frac{3}{2}$)2-$\frac{3}{2}$-3=$-\frac{15}{4}$,
函数的最大值为f(-$\frac{3}{2}$)=$\frac{1}{3}$•(-$\frac{3}{2}$)2+$\frac{3}{2}$-3=$\frac{3}{4}$.
点评 本题主要考查导数的计算,以及利用导数研究函数的最值,要求熟练掌握掌握常见函数的导数公式,比较基础.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
17.已知A={a,b},B={x|x⊆A},则A与B的关系是( )
| A. | A=B | B. | A⊆B | C. | B⊆A | D. | A∈B |
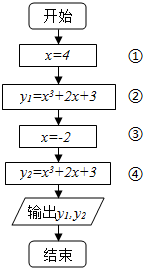 阅读如图所示的程序框图,回答下面的问题:
阅读如图所示的程序框图,回答下面的问题: