题目内容
已知不等式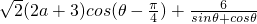 -2sin2θ<3a+6对于
-2sin2θ<3a+6对于 恒成立,求a的取值范围.
恒成立,求a的取值范围.
解:设sinθ+cosθ=x,则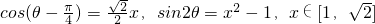
从而原不等式可化为:
即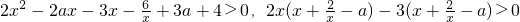 ,
,
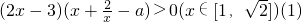
∴原不等式等价于不等式(1)∵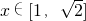 ,∴2x-3<0
,∴2x-3<0
(1)不等式恒成立等价于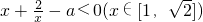 恒成立.
恒成立.
从而只要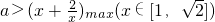 .
.
又容易知道 在
在 上递减,∴
上递减,∴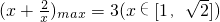 .
.
所以a>3.
分析:设sinθ+cosθ=x,则原不等式可化为: ,然后转化成
,然后转化成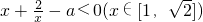 恒成立,将a分离出来,从而只要
恒成立,将a分离出来,从而只要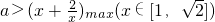 ,根据函数的单调性求出
,根据函数的单调性求出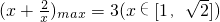 即可求出a的范围.
即可求出a的范围.
点评:本题主要考查了三角函数中的恒等变换应用,以及换元法的应用,解题的关键是恒等式的转化变形,以及利用函数的单调性求最值,是一道综合题.
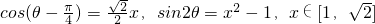
从而原不等式可化为:

即
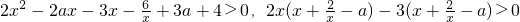 ,
,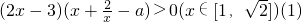
∴原不等式等价于不等式(1)∵
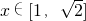 ,∴2x-3<0
,∴2x-3<0(1)不等式恒成立等价于
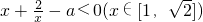 恒成立.
恒成立.从而只要
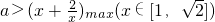 .
.又容易知道
 在
在 上递减,∴
上递减,∴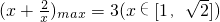 .
.所以a>3.
分析:设sinθ+cosθ=x,则原不等式可化为:
 ,然后转化成
,然后转化成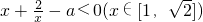 恒成立,将a分离出来,从而只要
恒成立,将a分离出来,从而只要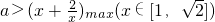 ,根据函数的单调性求出
,根据函数的单调性求出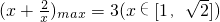 即可求出a的范围.
即可求出a的范围.点评:本题主要考查了三角函数中的恒等变换应用,以及换元法的应用,解题的关键是恒等式的转化变形,以及利用函数的单调性求最值,是一道综合题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
 选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)