题目内容
选做题(本题共2小题,任选一题作答,若做两题,则按所做的第①题给分)(1)已知不等式|x+1|-a<|x-2|的解集为(-∞,2),则a的值为
(2)曲线C1:ρ=2sinθ与曲线C2:ρ=2cosθ(ρ≥0,0≤θ<2π)的交点的极坐标为 .
【答案】分析:(1)不等式|x+1|-a<|x-2|的解集为(-∞,2),说明2是方程|x+1|-a=|x-2|的一个根,从而有 3-a=0,由此求得a的值.
(2)由ρ=2sinθ=2cosθ,且ρ≥0,0≤θ<2π,可 得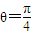 ,ρ=
,ρ=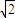 ,从而得一个交点的极坐标,再由极点也是它们的交点,可得它们的交点极坐标.
,从而得一个交点的极坐标,再由极点也是它们的交点,可得它们的交点极坐标.
解答:解:(1)不等式|x+1|-a<|x-2|的解集为(-∞,2),说明2是方程|x+1|-a=|x-2|的一个根,
∴3-a=0,故a=3.
(2)由ρ=2sinθ=2cosθ,且ρ≥0,0≤θ<2π,可 得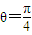 ,ρ=
,ρ=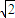 ,从而 得交点的极坐标为
,从而 得交点的极坐标为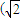 ,
,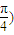 .
.
又因为极点也是它们的交点,所以它们的交点极坐标为:(0,0),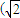 ,
,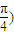 .
.
点评:本题主要考查绝对值不等式的解法,根据两条曲线的极坐标方程求出它们的交点的极坐标,属于基础题.
(2)由ρ=2sinθ=2cosθ,且ρ≥0,0≤θ<2π,可 得
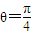 ,ρ=
,ρ=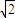 ,从而得一个交点的极坐标,再由极点也是它们的交点,可得它们的交点极坐标.
,从而得一个交点的极坐标,再由极点也是它们的交点,可得它们的交点极坐标.解答:解:(1)不等式|x+1|-a<|x-2|的解集为(-∞,2),说明2是方程|x+1|-a=|x-2|的一个根,
∴3-a=0,故a=3.
(2)由ρ=2sinθ=2cosθ,且ρ≥0,0≤θ<2π,可 得
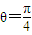 ,ρ=
,ρ=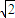 ,从而 得交点的极坐标为
,从而 得交点的极坐标为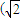 ,
,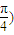 .
.又因为极点也是它们的交点,所以它们的交点极坐标为:(0,0),
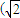 ,
,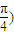 .
.点评:本题主要考查绝对值不等式的解法,根据两条曲线的极坐标方程求出它们的交点的极坐标,属于基础题.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 [选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.
[选做题]本题包括A、B、C、D共4小题,请从这4小题中选做2小题,每小题10分,共20分.