题目内容
已知集合 =( )
=( )A.
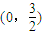
B.

C.
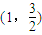
D.(0,1)
【答案】分析:根据指数函数的单调性知,2x2<3x,可得x的取值范围,即得到集合M.又根据对数函数的单调性可知0<x-1<1,得到集合N,最终求出答案.
解答:解:由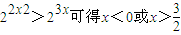
又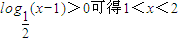
故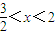
故选B.
点评:本题主要考查指数函数和对数函数的单调性问题.当底数大于1时单调递增,当底数大于0小于1时单调递减.
解答:解:由
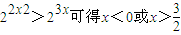
又
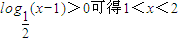
故
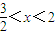
故选B.
点评:本题主要考查指数函数和对数函数的单调性问题.当底数大于1时单调递增,当底数大于0小于1时单调递减.

练习册系列答案
相关题目