题目内容
三棱锥S-ABC中,∠SBA=∠SCA=90°,△ABC是斜边AB=a的等腰直角三角形,且SB=BC,则以下结论中: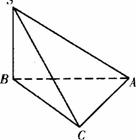
①异面直线SB与AC所成的角为90°;
②直线SB上平面ABC;
③二面角S-AC-B的大小为![]() ;
;
④点C到平面SAB的距离是![]() a.
a.
其中正确结论的序号是_____________.
答案:①②③④ 【解析】本题考查空间线面和面面垂直的证明及点面距离的求解等知识.由AC⊥BC,AC⊥SC可证得AC⊥平面SBC,所以AC⊥SB,所以①正确;又由SB⊥BA,可证得SB⊥平面ABC,②正确;因为SC⊥AC,BC⊥AC,所以∠SCB为二面角S-AC-B的平面角,SB=BC,所以∠SCB=![]() ,③正确;由SB⊥平面ABC,SB
,③正确;由SB⊥平面ABC,SB![]() 平面SAB,所以平面ABC上平面SAB,交线AB,取AB中点H,连CH,则CH⊥AB,所以CH⊥平面SAB,且CH=
平面SAB,所以平面ABC上平面SAB,交线AB,取AB中点H,连CH,则CH⊥AB,所以CH⊥平面SAB,且CH=![]() ,即点C到平面SAB的距离是
,即点C到平面SAB的距离是![]() ,④正确.
,④正确.

练习册系列答案
相关题目
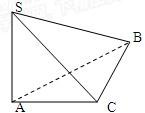 如图在三棱锥S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,
如图在三棱锥S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,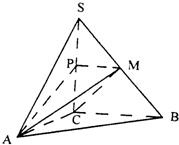 如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°.
如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°. 如图,在三棱锥S-ABC中,△ABC是边长为8的正三角形,
如图,在三棱锥S-ABC中,△ABC是边长为8的正三角形, 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2