题目内容
(1)已知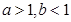 ,求证:
,求证: ;
;
(2)已知 ,且
,且 ,
,
求证: .
.
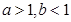 ,求证:
,求证: ;
;(2)已知
 ,且
,且 ,
,求证:
 .
.证明见解析.
试题分析:(1)本题证明只要利用作差法即可证得;(2)这个不等式比较复杂,考虑到不等式的形式,我们可用数学归纳法证明,关键在
 时的命题如何应用
时的命题如何应用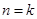 时的结论,
时的结论, 中要把两个括号合并成一个,又能应用
中要把两个括号合并成一个,又能应用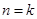 时的结论证明
时的结论证明 时的结论,当
时的结论,当 时,结论已经成立,当
时,结论已经成立,当 时,在
时,在 中可找到一个,不妨设为
中可找到一个,不妨设为 ,使
,使 ,即
,即 ,从而有
,从而有

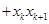
 ,这样代入进去可证得
,这样代入进去可证得 时结论成立.
时结论成立.(1)因为
 ,所以
,所以 ,即
,即 ; 2分
; 2分(2)证法一(数学归纳法):(ⅰ)当
 时,
时, ,不等式成立. 4分
,不等式成立. 4分(ⅱ)假设
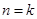 时不等式成立,即
时不等式成立,即 成立. 5分
成立. 5分则
 时,若
时,若 ,则命题成立;若
,则命题成立;若 ,则
,则 中必存在一个数小于1,不妨设这个数为
中必存在一个数小于1,不妨设这个数为 ,从而
,从而 ,即
,即 .
. 同理可得,
同理可得,所以

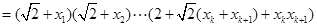

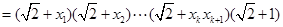
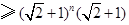

故
 时,不等式也成立. 9分
时,不等式也成立. 9分由(ⅰ)(ⅱ)及数学归纳法原理知原不等式成立. 10分
证法二:(恒等展开)左右展开,得

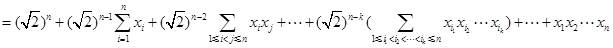 由平均值不等式,得
由平均值不等式,得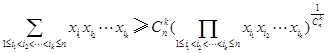
 8分
8分故


 . 10分
. 10分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,
, ,求证:
,求证: ,
, ,
, .
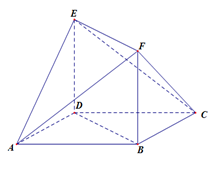
. 是菱形,
是菱形, 是矩形,
是矩形, 平面
平面 ,
, .
.
 平面
平面 ;
; 为直二面角,求直线
为直二面角,求直线 与平面
与平面 所成的角
所成的角 的正弦值.
的正弦值. ,求证:关于
,求证:关于 的三个方程
的三个方程 ,
, ,
,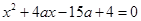 中至少有一个方程有实数根.
中至少有一个方程有实数根. ,(其中
,(其中 )
) 及
及 ;
; 与
与 的大小,并说明理由.
的大小,并说明理由. 有有理实数根,那么
有有理实数根,那么 ,
, ,
, 中至少有一个是偶数,下列假设中正确的是()
中至少有一个是偶数,下列假设中正确的是()