题目内容
已知双曲线C的方程为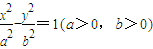
，它的左、右焦点分别F1，F2，左右顶点为A1，A2，过焦点F2先做其渐近线的垂线，垂足为p，再作与x轴垂直的直线与曲线C交于点Q，R，若PF2，A1A2，QF1依次成等差数列，则离心率e=（ ）A．
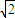
B．
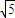
C．
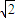或
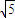
D．
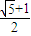
【答案】分析：由题设条件推导出|F2P|=b，|QF1|=2a-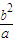
，|A1A2|=2a，由PF2，A1A2，QF1依次成等差数列，知b，2a，2a-
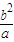依次成等差数列，由此能求出离心率e．
解答：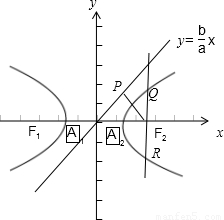
解：由题设知双曲线C的方程为
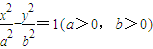的一条渐近线方程l：y=
，
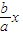∵右焦点F（c，0），∴F2P⊥l，
∴|F2P|=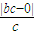
=b，
∵|F2Q|⊥x轴，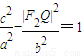
，解得|F2Q|=
，
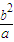∴|QF1|=2a-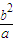
，
∵|A1A2|=2a，PF2，A1A2，QF1依次成等差数列，
∴b，2a，2a-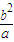
依次成等差数列，
∴4a=b+2a+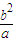
，
∴2=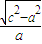
+
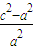，即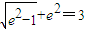
，
解得e=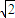
．
故选A．
点评：本题考查双曲线的离心率的求法，解题时要认真审题，注意点到直线的距离公式的灵活运用．
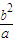，|A1A2|=2a，由PF2，A1A2，QF1依次成等差数列，知b，2a，2a-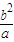依次成等差数列，由此能求出离心率e．解答：
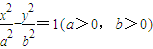解：由题设知双曲线C的方程为的一条渐近线方程l：y=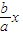，∵右焦点F（c，0），∴F2P⊥l，
∴|F2P|=
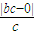=b，∵|F2Q|⊥x轴，
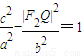，解得|F2Q|=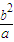，∴|QF1|=2a-
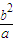，∵|A1A2|=2a，PF2，A1A2，QF1依次成等差数列，
∴b，2a，2a-
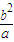依次成等差数列，∴4a=b+2a+
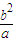，∴2=
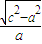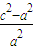+，即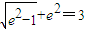，解得e=
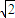．故选A．
点评：本题考查双曲线的离心率的求法，解题时要认真审题，注意点到直线的距离公式的灵活运用．
练习册系列答案
相关题目