题目内容
| |||||||||||||||
答案:B

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
| |||||
| |||||
| |||||||||||||||
记集合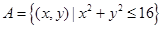 和集合
和集合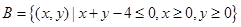 表示的平面区域分别为
表示的平面区域分别为 ,若在区域
,若在区域 内任取一点
内任取一点 ,则点M落在区域
,则点M落在区域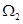 的概率为( )
的概率为( )
A.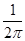 | B.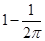 | C.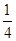 | D.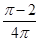 |
设全集 ,集合
,集合 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
题目内容
| |||||||||||||||

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
| |||||
| |||||
| |||||||||||||||
记集合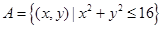 和集合
和集合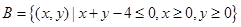 表示的平面区域分别为
表示的平面区域分别为 ,若在区域
,若在区域 内任取一点
内任取一点 ,则点M落在区域
,则点M落在区域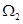 的概率为( )
的概率为( )
A.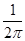 | B.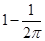 | C.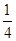 | D.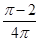 |
设全集 ,集合
,集合 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |