题目内容
.已知函数![]() (1)判定
(1)判定![]() 的单调性,并证明。
的单调性,并证明。
(2)设![]() ,若方程
,若方程![]() 有实根,求
有实根,求![]() 的取值范围。
的取值范围。
(3)求函数![]() 在
在![]() 上的最大值和最小值。
上的最大值和最小值。
(1)当x<-3时,当a>1时,f(x1)-f(x2)<0,∴f(x)在(![]() )上单调递增
)上单调递增
当0<a<1时,f(x1)-f(x2)>0, ∴f(x)在(![]() )上单调递减
)上单调递减
当x>3时,同理。(2)![]() ;(3)函数h(x)在[4,6]上的最为
;(3)函数h(x)在[4,6]上的最为![]() ,最大值为h(4)=-2。
,最大值为h(4)=-2。
解析:
(1)![]() ,当x<-3时,任取x1<x2<-3
,当x<-3时,任取x1<x2<-3
则![]() -
-![]() =
=![]() ,
,
∵(x1-3)(x2+3)-(x1+3)(x2-3)=6(x1-x2)<0,
又(x1-3)(x2+3)>0且(x1+3)(x2-3)>0
∴![]() <1
<1
∴当a>1时,f(x1)-f(x2)<0,∴f(x)在(![]() )上单调递增
)上单调递增
当0<a<1时,f(x1)-f(x2)>0, ∴f(x)在(![]() )上单调递减
)上单调递减
当x>3时,同理。
(2)若f(x)=g(x)有实根,即: ![]()
∴ ,∴方程
,∴方程![]() 有大于3的实根。
有大于3的实根。
∴![]()
=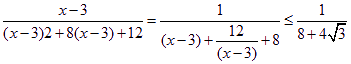
![]()
当且仅当![]() ,即
,即![]() “=”号成立
“=”号成立
∴![]() 。
。
(3)![]() ,
,![]()
由![]() 得x2-3x-4=0解得x1=4,x2=-1(舍去)
得x2-3x-4=0解得x1=4,x2=-1(舍去)
当![]() 时,
时,![]() 单调递减;
单调递减;
∴函数h(x)在[4,6]上的最为![]() ,最大值为h(4)=-2。
,最大值为h(4)=-2。

练习册系列答案
相关题目
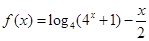 .
.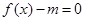 有解,求m的取值范围;
有解,求m的取值范围;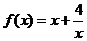 已知函数:
已知函数:  的奇偶性,并证明;
的奇偶性,并证明; 时,判断
时,判断 )上的单调性,并证明.
)上的单调性,并证明.