题目内容
(选修4—1几何证明选讲)已知:直线AB过圆心O,交⊙O于AB,直线AF交⊙O于F(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连结AC
 求证:(1)
求证:(1)![]() (2)AC2=AE·AF
(2)AC2=AE·AF
23(选修4—4坐标系与参数方程选讲)以直角坐标系的原点O为极点,![]() 轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线
轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线![]() 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角![]() .
.
(I)写出直线![]() 参数方程;
参数方程;
(II)设![]() 与圆
与圆![]() 相交于两点A、B,求点P到A、B两点的距离之积.
相交于两点A、B,求点P到A、B两点的距离之积.
24.选修4-5:不等式选讲
设函数![]() .
.
(Ⅰ)求不等式![]() 的解集;
的解集;
(Ⅱ)![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
证明:(1)连结BC,由AB为⊙O的直径所以![]() …………1分
…………1分
又因为![]() …………2分
…………2分
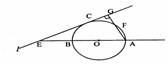 又因为GC与⊙O相切于C,、所以
又因为GC与⊙O相切于C,、所以![]() …………4分
…………4分
所以![]() …………6分
…………6分
(2)由(1)可知![]() ,连结CF
,连结CF
又因为GE与⊙O相切于C,所以![]() 所以
所以![]()
所以![]() …………8分
…………8分
所以![]() 所以
所以![]() …………10分
…………10分
23.解:(I)直线的参数方程是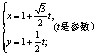 .……………………… 3分
.……………………… 3分
(II)因为点A,B都在直线L上,所以可设它们对应的参数为![]() 则点A,B的坐标分别为
则点A,B的坐标分别为![]()
![]() . …………………………… 5分
. …………………………… 5分
圆![]() 化为直角坐标系的方程
化为直角坐标系的方程![]() .…………………………… 7分
.…………………………… 7分
以直线l的参数方程代入圆的方程![]() 整理得到
整理得到![]() ①
①
因为![]() 是方程①的解,从而
是方程①的解,从而![]() =-2.---------------9分
=-2.---------------9分
所以|PA|·|PB|=![]() =|-2|=2. …………………………… 10分
=|-2|=2. …………………………… 10分
24.解:(Ⅰ)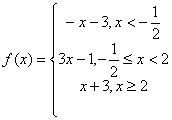 ,------------------------------------------------2分
,------------------------------------------------2分
当![]()
当![]()
当![]()
综上所述 ![]() ------------------------------------------------------------5分
------------------------------------------------------------5分
(Ⅱ)易得![]() ,若
,若![]() ,
,![]() 恒成立,
恒成立,
则只需![]() ,
,
综上所述![]() -------------------------------------------------------------------------10分
-------------------------------------------------------------------------10分

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案 A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线
A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线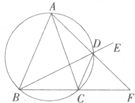 已知△ABC中AB=AC,D为△ABC外接圆劣弧,
已知△ABC中AB=AC,D为△ABC外接圆劣弧,
 (2013•辽宁)(选修4-1几何证明选讲)
(2013•辽宁)(选修4-1几何证明选讲) (2011•南京模拟)A.选修4-1几何证明选讲
(2011•南京模拟)A.选修4-1几何证明选讲