题目内容
(本小题满分12分)
已知函数f(x)=Asin(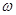 x+
x+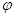 )(x∈R,
)(x∈R,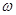 >0, 0<
>0, 0<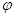 <
<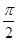 )的部分图象如图所示。
)的部分图象如图所示。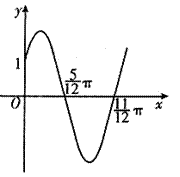
(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x- )的单调递增区间。
)的单调递增区间。
(1) f(x)=2sin(2x+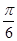 )
)
(2) g(x)的单调递增区间是[k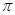 -
-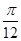 ,k
,k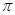 +
+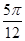 ],k∈z.
],k∈z.
解析试题分析:解:(1)由题设图象知,周期T=2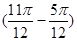 =
=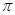 ,所以
,所以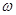 =
=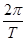 =2,
=2,
因为点(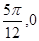 )在函数图象上,所以Asin(2×
)在函数图象上,所以Asin(2×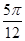 +
+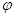 )=0,即sin(
)=0,即sin(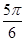 +
+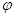 )=0。
)=0。
又因为0<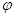 <
<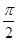 ,所以
,所以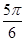 <
<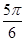 +
+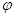 <
<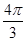 ,从而
,从而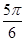 +
+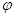 =
=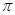 ,即
,即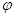 =
=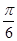 .
.
又点(0,1)在函数图象上,所以Asin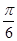 =1,A="2."
=1,A="2."
故函数f(x)的解析式为f(x)=2sin(2x+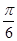 ).
).
(2)g(x)=2sin[2(x- +
+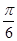 ]=2sin(2x-
]=2sin(2x-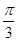 ),
),
由2k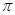 -
-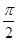 ≤2x-
≤2x-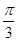 ≤2k
≤2k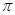 +
+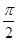 ,得k
,得k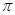 -
-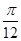 ≤x≤k
≤x≤k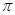 +
+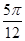 ,k∈z.
,k∈z.
所以g(x)的单调递增区间是[k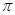 -
-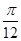 ,k
,k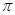 +
+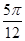 ],k∈z.
],k∈z.
考点:三角函数的性质
点评:解决该试题的关键是对数函数性质的灵活运用,能结合三角函数的性质来求解单调区间,属于基础题。

练习册系列答案
相关题目
 中,已知
中,已知 ,
,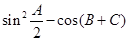 的值;
的值; ,
, ,求
,求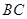 的长。
的长。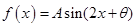 ,其中
,其中 请分别解答以下两小题.
请分别解答以下两小题. ,求函数
,求函数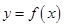 的解析式.
的解析式.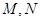 分别是函数
分别是函数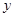 轴两侧与
轴两侧与 轴的两个相邻交点, 函数图像上的一点
轴的两个相邻交点, 函数图像上的一点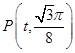 ,若满足
,若满足 ,求函数
,求函数 的最大值.
的最大值.
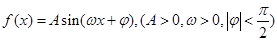 的最小正周期为
的最小正周期为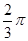 ,最小值为
,最小值为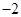 ,图象过点
,图象过点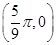 ,(1)求
,(1)求 的解析式;(2)求满足
的解析式;(2)求满足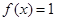 且
且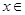
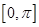 的
的 的集合.
的集合.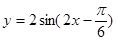 .
.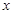 的取值集合,并写出最大值。
的取值集合,并写出最大值。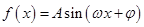
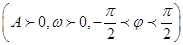 一个周期的图像如图所示。
一个周期的图像如图所示。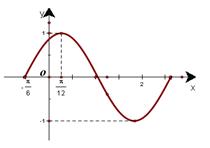
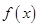 的表达式;
的表达式;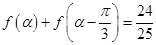 ,且
,且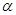 为
为 的一个内角,求
的一个内角,求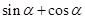 的值。
的值。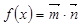 ,其中
,其中 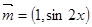 ,
,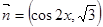 ,在
,在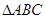 中,
中, 分别是角
分别是角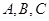 的对边,且
的对边,且 ,
,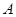 ;(2)若
;(2)若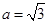 ,
,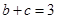 ,求
,求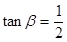 ,
,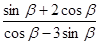 的值;
的值;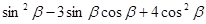 的值。
的值。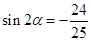 ,
,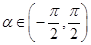 ,求
,求 的值;
的值;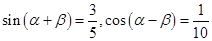 .求
.求 的值.
的值.