题目内容
四棱锥P—ABCD的底面是边长为a的正方形,PB⊥面ABCD.
(1)若面PAD与面ABCD所成的二面角为60°,求这个四棱锥的体积;
(2)证明无论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°
(Ⅰ)![]() (Ⅱ)证明见解析
(Ⅱ)证明见解析
解析:
(1)正方形ABCD是四棱锥P—ABCD的底面, 其面积为![]() 从而只要算出四棱锥的高就行了.
从而只要算出四棱锥的高就行了.
![]() 面ABCD,
面ABCD,
∴BA是PA在面ABCD上的射影.又DA⊥AB,
∴PA⊥DA,
∴∠PAB是面PAD与面ABCD所成的二面角的平面角,
∠PAB=60°.
而PB是四棱锥P—ABCD的高,PB=AB·tg60°=![]() a,
a,
![]() .
.
(2)不论棱锥的高怎样变化,棱锥侧面PAD与PCD恒为全等三角形.
作AE⊥DP,垂足为E,连结EC,则△ADE≌△CDE,
![]() 是面PAD与面PCD所成的二面角的平面角.
是面PAD与面PCD所成的二面角的平面角.
设AC与DB相交于点O,连结EO,则EO⊥AC,
![]()
在![]()
故平面PAD与平面PCD所成的二面角恒大于90°.


练习册系列答案
相关题目
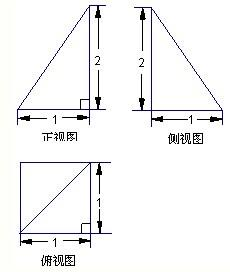 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
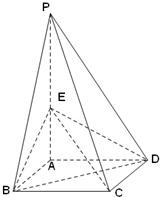 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: