题目内容
(本小题满分12分)如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC.

(1) 求证:平面AB1C1⊥平面AC1;
(2) 若AB1⊥A1C,求线段AC与AA1长度之比;
(3) 若D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,试确定点E的位置;若不存在,请说明理由.
【答案】
(1)只需证B1C1⊥平面AC1 .(2)1:1.(3)点E位于AB的中点时。
【解析】
试题分析:(1)由于ABC-A1B1C1是直三棱柱,所以B1C1⊥CC1;
又因为AC⊥BC ,所以B1C1⊥A1C1,所以B1C1⊥平面AC1 .
由于B1C1 平面AB1C1,从而平面AB1C1⊥平面AC1 .
平面AB1C1,从而平面AB1C1⊥平面AC1 .
(2)由(1)知,B1C1⊥A1C .所以,若AB1⊥A1C,则可
得:A1C⊥平面AB1C1,从而A1C⊥ AC1 .
由于ACC1A1是矩形,故AC与AA1长度之比为1:1.
(3)点E位于AB的中点时,能使DE∥平面AB1C1.
证法一:设F是BB1的中点,连结DF、EF、DE.则易证:平面DEF//平面AB1C1,从而
DE∥平面AB1C1.
证法二:设G是AB1的中点,连结EG,则易证EG DC1. 所以DE// C1G,DE∥平面AB1C1.
DC1. 所以DE// C1G,DE∥平面AB1C1.
考点:面面垂直的判定定理;线面平行的判定定理;线面垂直的判定定理。
点评:证明线面平行的常用方法:
①定义:若一条直线和一个平面没有公共点,则它们平行;
②线线平行Þ线面平行
若平面外的一条直线平行于平面内的一条直线,则它与这个平面平行。
 即
即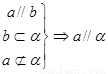
③面面平行Þ线面平行
若两平面平行,则其中一个平面内的任一条直线平行于另一个平面。
 即
即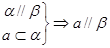

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目