题目内容
已知a是实数,则函数f(x)=acosax-1的图象不可能是( )
分析:利用三角函数的图象和性质,通过周期和最值是否对应进行判断.
解答:解:A.最大值为0<a-1<1,即1<a<2,
<
<1,周期T=
∈(π,2π),有可能.
B.最大值为0<a-1<1,即1<a<2,
<
<1,周期T=
∈(π,2π),有可能.
C.当a=0时,f(x)=acosax-1=-1,图象成立.
D.最大值为-1<a-1<0,即0<a<1,
>1,周期T=
>2π,由图象可知,D中的周期不对应.
故选D.
| 1 |
| 2 |
| 1 |
| a |
| 2π |
| a |
B.最大值为0<a-1<1,即1<a<2,
| 1 |
| 2 |
| 1 |
| a |
| 2π |
| a |
C.当a=0时,f(x)=acosax-1=-1,图象成立.
D.最大值为-1<a-1<0,即0<a<1,
| 1 |
| a |
| 2π |
| a |
故选D.
点评:本题主要考查三角函数的图象和性质,利用三角函数的周期和最值之间的关系是否对应是解决本题的关键.

练习册系列答案
相关题目
已知a是实数,则函数f(x)=1+asinax的图象不可能是( )
A、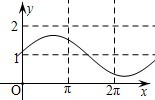 | B、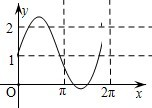 | C、 | D、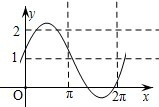 |