题目内容
已知双曲线的中心在原点,以两条坐标轴为对称轴,离心率是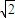 ,两准线间的距离大于
,两准线间的距离大于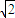 ,且双曲线上动点P到A(2,0)的最近距离为1.
,且双曲线上动点P到A(2,0)的最近距离为1.(Ⅰ)求证:该双曲线的焦点不在y轴上;
(Ⅱ)求双曲线的方程;
(Ⅲ)如果斜率为k的直线L过点M(0,3),与该双曲线交于A、B两点,若
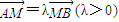 ,试用l表示k2,并求当
,试用l表示k2,并求当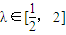 时,k的取值范围.
时,k的取值范围.
【答案】分析:(1)反证法:假设双曲线的焦点在y轴上,因为双曲线上任一点到点A(2,0)的距离大于点A到渐近线的距离,
而点A到渐近线的距离大于1,这与“双曲线上动点P到A(2,0)的最近距离为1”矛盾,故假设不对.
(2)双曲线的焦点在x轴上,设出方程,待定系数法求方程.
(3)直线方程与双曲线方程联立,化为一元二次方程,应用根与系数的关系、2个向量关系,用λ表示k2,
由λ范围,求k的取值范围.
解答:证明:(Ⅰ)设双曲线的实轴长为2a,虚轴长为2b,焦距为2c,
由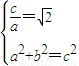 ,得c=
,得c=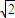 a,a=b,
a,a=b,
∴双曲线的渐近线方程为y=±x.
若双曲线的焦点在y轴上,
则双曲线上任一点到点A(2,0)的距离大于点A到渐近线的距离,
而点A到渐近线的距离d=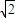 >1,
>1,
这与“双曲线上动点P到A(2,0)的最近距离为1”矛盾.
所以双曲线的焦点不在y轴上.
方法二:联立双曲线方程y2-x2=a2与圆(x-2)2+y2=1,证明方程组无解.
解:(Ⅱ)由(Ⅰ)知,双曲线的焦点在x轴上,
设双曲线的方程为x2-y2=a2,P(x,y),则x2-y2=a2,
|PA|2=(x-2)2+y2=(x-2)2+x2-a2=2(x-1)2+2-a2,
又由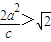 得a>1
得a>1
又当x=a时,|PA|2有最小值,即2(a-1)2+2-a2=(a-2)2=1,
∴a=3,所以,双曲线的方程为x2-y2=9.
解(Ⅲ):设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2)
∵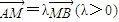 ,∴(-x1,3-y1)=λ(x2,y2-3),∴x1=-λx2(x1x2<0)①,
,∴(-x1,3-y1)=λ(x2,y2-3),∴x1=-λx2(x1x2<0)①,
由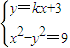 消去y得,(1-k2)x2-6kx-18=0,
消去y得,(1-k2)x2-6kx-18=0,
x1+x2=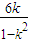 ②,x1x2=
②,x1x2=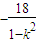 <0 ③
<0 ③
将①分别代入②、③
得,(1-λ)x2=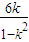 ④λx22=
④λx22=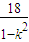 ⑤
⑤
④2÷⑤并整理得,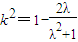 (l>0)
(l>0)
令f(l)=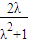 ,则
,则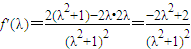
令f′(λ)=0,得 λ=1; 令f′(λ)>0,
得0<l<1;令f′(λ)<0,得l>1
当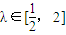 时,
时,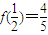 ,
,
f(1)=1,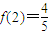 ,∴
,∴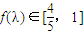
∴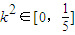 ,∴
,∴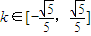 .(13分)
.(13分)
点评:本题考查直线与圆锥曲线的综合应用.
而点A到渐近线的距离大于1,这与“双曲线上动点P到A(2,0)的最近距离为1”矛盾,故假设不对.
(2)双曲线的焦点在x轴上,设出方程,待定系数法求方程.
(3)直线方程与双曲线方程联立,化为一元二次方程,应用根与系数的关系、2个向量关系,用λ表示k2,
由λ范围,求k的取值范围.
解答:证明:(Ⅰ)设双曲线的实轴长为2a,虚轴长为2b,焦距为2c,
由
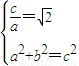 ,得c=
,得c=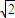 a,a=b,
a,a=b,∴双曲线的渐近线方程为y=±x.
若双曲线的焦点在y轴上,
则双曲线上任一点到点A(2,0)的距离大于点A到渐近线的距离,
而点A到渐近线的距离d=
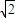 >1,
>1,这与“双曲线上动点P到A(2,0)的最近距离为1”矛盾.
所以双曲线的焦点不在y轴上.
方法二:联立双曲线方程y2-x2=a2与圆(x-2)2+y2=1,证明方程组无解.
解:(Ⅱ)由(Ⅰ)知,双曲线的焦点在x轴上,
设双曲线的方程为x2-y2=a2,P(x,y),则x2-y2=a2,
|PA|2=(x-2)2+y2=(x-2)2+x2-a2=2(x-1)2+2-a2,
又由
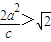 得a>1
得a>1又当x=a时,|PA|2有最小值,即2(a-1)2+2-a2=(a-2)2=1,
∴a=3,所以,双曲线的方程为x2-y2=9.
解(Ⅲ):设直线l的方程为y=kx+3,A(x1,y1),B(x2,y2)
∵
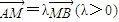 ,∴(-x1,3-y1)=λ(x2,y2-3),∴x1=-λx2(x1x2<0)①,
,∴(-x1,3-y1)=λ(x2,y2-3),∴x1=-λx2(x1x2<0)①,由
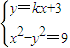 消去y得,(1-k2)x2-6kx-18=0,
消去y得,(1-k2)x2-6kx-18=0,x1+x2=
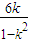 ②,x1x2=
②,x1x2=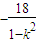 <0 ③
<0 ③将①分别代入②、③
得,(1-λ)x2=
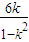 ④λx22=
④λx22=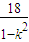 ⑤
⑤④2÷⑤并整理得,
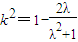 (l>0)
(l>0)令f(l)=
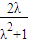 ,则
,则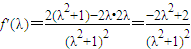
令f′(λ)=0,得 λ=1; 令f′(λ)>0,
得0<l<1;令f′(λ)<0,得l>1
当
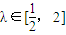 时,
时,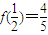 ,
,f(1)=1,
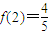 ,∴
,∴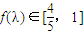
∴
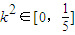 ,∴
,∴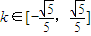 .(13分)
.(13分)点评:本题考查直线与圆锥曲线的综合应用.

练习册系列答案
相关题目