题目内容
已知点p（x，y）是直线kx+y+4=0（k＞0）上一动点，PA、PB是圆C：x2+y2-2y=0的两条切线，A、B是切点，若四边形PACB的最小面积是2，则k的值为
2
2
．分析：先求圆的半径，四边形PACB的最小面积是2，转化为三角形PBC的面积是1，求出切线长，再求PC的距离也就是圆心到直线的距离，可解k的值．
解答：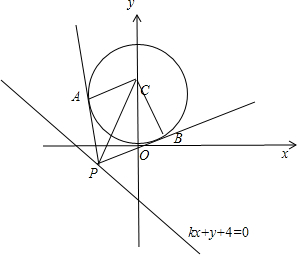
解：圆C：x2+y2-2y=0的圆心（0，1），半径是r=1，
由圆的性质知：S四边形PACB=2S△PBC，四边形PACB的最小面积是2，
∴S△PBC的最小值S=1=
rd（d是切线长）
∴d最小值=2
圆心到直线的距离就是PC的最小值，
=
=
∵k＞0，∴k=2
故 答案为：2
解：圆C：x2+y2-2y=0的圆心（0，1），半径是r=1，由圆的性质知：S四边形PACB=2S△PBC，四边形PACB的最小面积是2，
∴S△PBC的最小值S=1=
| 1 |
| 2 |
∴d最小值=2
圆心到直线的距离就是PC的最小值，
| 12+ 22 |
| 5 | ||
|
| 5 |
∵k＞0，∴k=2
故 答案为：2
点评：本题考查直线和圆的方程的应用，点到直线的距离公式等知识，是中档题．
练习册系列答案
相关题目