题目内容
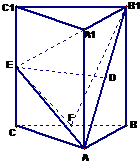 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D,E,F分别是B1A,CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D,E,F分别是B1A,CC1,BC的中点.(1)求证:B1F⊥平面AEF;
(2)求二面角B1-AE-F的正切值.
分析:(1)由已知中三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D,E,F分别是B1A,CC1,BC的中点,结合等腰三角形性质及直三棱柱的几何特征,我们易判断出AF⊥B1F,B1F⊥EF,进而根据线面垂直的判定定理即可得到B1F⊥平面AEF;
(2)B1M⊥AE于M,连接FM,由三垂线定理我们易得∠B1MF即为二面角B1-AE-F的平面角,解三角形B1MF,即可求出二面角B1-AE-F的正切值.
(2)B1M⊥AE于M,连接FM,由三垂线定理我们易得∠B1MF即为二面角B1-AE-F的平面角,解三角形B1MF,即可求出二面角B1-AE-F的正切值.
解答:证明:(1)等腰直角三角形△ABC中F为斜边的中点,
∴AF⊥BC
又∵直三棱柱ABC-A1B1C1,
∴面ABC⊥面BB1C1C,
∴AF⊥面C1B,
∴AF⊥B1F
设AB=AA1=1,
∴B1F=
,EF=
,B1E=
,
∴B1F2+EF2=B1E2,
∴B1F⊥EF
又AF∩EF=F,
∴B1F⊥面AEF
解:(2)∵B1F⊥面AEF,
作B1M⊥AE于M,连接FM,
∴∠B1MF为所求
又∵FM=
,
所求二面的正切值为
∴AF⊥BC
又∵直三棱柱ABC-A1B1C1,
∴面ABC⊥面BB1C1C,
∴AF⊥面C1B,
∴AF⊥B1F
设AB=AA1=1,
∴B1F=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
∴B1F2+EF2=B1E2,
∴B1F⊥EF
又AF∩EF=F,
∴B1F⊥面AEF
解:(2)∵B1F⊥面AEF,
作B1M⊥AE于M,连接FM,
∴∠B1MF为所求
又∵FM=
| ||
|
所求二面的正切值为
| 5 |
点评:本题考查的知识点是直线与平面垂直的判定及二面角的平面角的求法,其中在求二面角时,找出二面角的平面角是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=