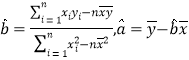题目内容
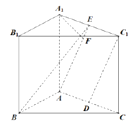
【题目】如图,直三棱柱![]() 中,
中,![]() 分别为
分别为![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)法一:要证![]() 平面
平面![]() ,只需证明
,只需证明![]() 即可,通过构造平行四边形可证之;
即可,通过构造平行四边形可证之;
法二:可先证平面![]() 平面
平面![]() ,利用面面平行的性质即可得到
,利用面面平行的性质即可得到![]() 平面
平面![]() ;
;
(2)法一:由于![]() 即为
即为![]() 与平面
与平面![]() 所成的角,利用数据求之;
所成的角,利用数据求之;
法二:(等积法)利用等积法计算出![]() 到平面
到平面![]() 的距离,从而要求的答案为:
的距离,从而要求的答案为:![]() 即可.
即可.
(1)法一:取![]() 中点
中点![]() ,连接
,连接![]() ,在直三棱柱
,在直三棱柱![]() 中,
中,![]() .
.
∵![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .∵
.∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
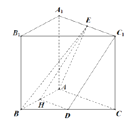
法二:取![]() 中点
中点![]() ,连结
,连结![]() ,在直三棱柱
,在直三棱柱![]() 中,
中,![]() .
.
∵![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 分别为
分别为![]() 中点,∴
中点,∴![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
![]() 平面
平面![]() 平面
平面![]() .
.![]() 平面
平面![]() 平面
平面![]() .
.
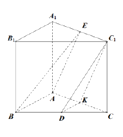
(2)法一:直三棱柱![]() 中,
中,![]() 平面
平面![]() ,∴
,∴![]() .
.
又∵![]() ,且
,且![]() ,∴
,∴![]() 平面
平面![]() .
.
过![]() 作
作![]() 于
于![]() .∵
.∵![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() 平面
平面![]() .
.
又![]() 即为
即为![]() 与平面
与平面![]() 所成的角.
所成的角.
![]() .
.
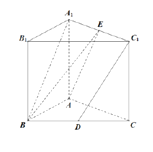
法二:(等积法)![]() 与平面
与平面![]() 所成的角相等.
所成的角相等.
连结![]() ,直三棱柱
,直三棱柱![]() 中,
中,![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() 平面
平面![]() .
.
![]() ,
,![]() .
.
设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,![]() .
.
∵![]() ,即
,即![]() .
.
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
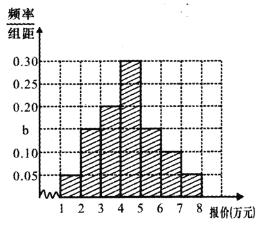
【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在![]() 分以下的学生后,共有男生
分以下的学生后,共有男生![]() 名,女生
名,女生![]() 名.现采用分层抽样的方法,从中抽取了
名.现采用分层抽样的方法,从中抽取了![]() 名学生,按性别分为两组,并将两组学生成绩分为
名学生,按性别分为两组,并将两组学生成绩分为![]() 组,得到如下所示频数分布表.
组,得到如下所示频数分布表.
分数段 |
|
|
|
|
|
|
男 |
|
|
|
|
|
|
女 |
|
|
|
|
|
|
(Ⅰ)规定![]() 分以上为优分(含
分以上为优分(含![]() 分),请你根据已知条件作出
分),请你根据已知条件作出![]() 列联表.
列联表.
优分 | 非优分 | 合计 | |
男生 | |||
女生 | |||
合计 |
|
(Ⅱ)根据你作出的![]() 列联表判断是否有
列联表判断是否有![]() 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式:
|
|
|
|
|
|
|
|
|
|
 ,其中
,其中![]() .
.