题目内容
已知数列{an}是以d为公差的等差数列,数列{bn}是以q为公比的等比数列
(Ⅰ)若数列{bn}的前n项和为Sn,且a1=b1=d=2,S3<5b2+a88-180,求整数q的值(Ⅱ)在(Ⅰ)的条件下,试问数列{bn}中是否存在一项bk,使得b,k恰好可以表示为该数列中连续P(P∈N,P≥2)项和?请说明理由。
(Ⅲ)若b1=ar,b2=as≠ar, b3=at(其中t>s>r,且(s-r)是(t-r)的约数)
求证:数列{bn}中每一项都是数列{an}中的项.
(Ⅰ)若数列{bn}的前n项和为Sn,且a1=b1=d=2,S3<5b2+a88-180,求整数q的值(Ⅱ)在(Ⅰ)的条件下,试问数列{bn}中是否存在一项bk,使得b,k恰好可以表示为该数列中连续P(P∈N,P≥2)项和?请说明理由。
(Ⅲ)若b1=ar,b2=as≠ar, b3=at(其中t>s>r,且(s-r)是(t-r)的约数)
求证:数列{bn}中每一项都是数列{an}中的项.
解:(Ⅰ)由题意知an=2n,bn=2·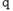 n-1
n-1
∴由S3<5b2+a88-180得.
b1+b2+b3<a88+5b2-180 b1-4b2+b3<176-180
b1-4b2+b3<176-180 q2-4q+3<0
q2-4q+3<0
解得1<q<3,q为值数,∴q=2.
(Ⅱ)假设数列{bn}中存在一项bk满足bk=bm+bm+1+……bm+p-1
∴bn=2n ∴bk>bm+p-1 2k>2m+p-1
2k>2m+p-1 k>m+p-1
k>m+p-1 k≥m+p.
k≥m+p.
又bk=2k=bm+bm+1=2m+2m+1+2m+p-1=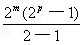 =2m+p-2m
=2m+p-2m
∴2k<2m+p k<m+p与k≥m+p矛盾,
k<m+p与k≥m+p矛盾,
∴不存在
(Ⅲ)由b1=ar得b2=b1q=arq=as=ar+(s-r)d,则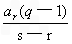 d=
d=
又b3=b1q2=ar.q2=at=ar+(t-r)d arq2-ar=(t-r)
arq2-ar=(t-r)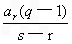
 ar(q+1)(q-1)=ar(q-1).
ar(q+1)(q-1)=ar(q-1).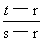
∵as≠ar b1≠b2 ∴q≠1.
b1≠b2 ∴q≠1.
又ar≠0 故q=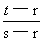 -1又t>s>r且(s-r)是(t-r)的约数
-1又t>s>r且(s-r)是(t-r)的约数
∴q是正整数且q≥2
对于数列{bn}中任一项bi(这里只讨论i>3的情形),
有bi=arqi-1= ar+ar(qi-1-1)= ar+ ar(q-1)(1+q+…+qi-2)
= ar+d(s-r)(1+q+…+qi-2)=ar+[((s-r)(1+q+…+qi+2)+1)-1]d
由于(s-r)(1+q+…+qi-2)+1为正整数
∴bi一定是数列{an}中的项
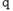 n-1
n-1 ∴由S3<5b2+a88-180得.
b1+b2+b3<a88+5b2-180
 b1-4b2+b3<176-180
b1-4b2+b3<176-180 q2-4q+3<0
q2-4q+3<0 解得1<q<3,q为值数,∴q=2.
(Ⅱ)假设数列{bn}中存在一项bk满足bk=bm+bm+1+……bm+p-1
∴bn=2n ∴bk>bm+p-1
 2k>2m+p-1
2k>2m+p-1 k>m+p-1
k>m+p-1 k≥m+p.
k≥m+p.又bk=2k=bm+bm+1=2m+2m+1+2m+p-1=
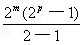 =2m+p-2m
=2m+p-2m ∴2k<2m+p
 k<m+p与k≥m+p矛盾,
k<m+p与k≥m+p矛盾,∴不存在
(Ⅲ)由b1=ar得b2=b1q=arq=as=ar+(s-r)d,则
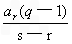 d=
d= 又b3=b1q2=ar.q2=at=ar+(t-r)d
 arq2-ar=(t-r)
arq2-ar=(t-r)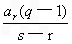
 ar(q+1)(q-1)=ar(q-1).
ar(q+1)(q-1)=ar(q-1).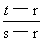
∵as≠ar
 b1≠b2 ∴q≠1.
b1≠b2 ∴q≠1.又ar≠0 故q=
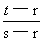 -1又t>s>r且(s-r)是(t-r)的约数
-1又t>s>r且(s-r)是(t-r)的约数 ∴q是正整数且q≥2
对于数列{bn}中任一项bi(这里只讨论i>3的情形),
有bi=arqi-1= ar+ar(qi-1-1)= ar+ ar(q-1)(1+q+…+qi-2)
= ar+d(s-r)(1+q+…+qi-2)=ar+[((s-r)(1+q+…+qi+2)+1)-1]d
由于(s-r)(1+q+…+qi-2)+1为正整数
∴bi一定是数列{an}中的项

练习册系列答案
相关题目