题目内容
已知函数f(x)=|x2-1|,g(x)=k|x-1|.
(Ⅰ)已知0<m<n,若f(m)=f(n),求m2+n2的值;
(Ⅱ)设F(x)=
,当k=
时,求F(x)在(-∞,0)上的最小值;
(Ⅲ)求函数G(x)=f(x)+g(x)在区间[-2,2]上的最大值.
(Ⅰ)已知0<m<n,若f(m)=f(n),求m2+n2的值;
(Ⅱ)设F(x)=
|
| 1 |
| 2 |
(Ⅲ)求函数G(x)=f(x)+g(x)在区间[-2,2]上的最大值.
分析:(Ⅰ)将f(x)化为分段函数,利用分段函数的图象,可知0≤m<1<n≤
,再根据f(m)=f(n),可以得到m与n的关系,即可得m2+n2的值;
(Ⅱ)根据f(x)和g(x)的函数解析式,分类表示出F(x)的解析式,写成分段函数,再根据分段函数的解析式,即可求出F(x)在(-∞,0)上的最小值;
(Ⅲ)根据f(x)和g(x)的函数解析式,求出G(x)的解析式,再分别针对每一段上的解析式分别求解最值,在对每一段中的最值进行分类比较,确定其中的最大值,即可求得函数G(x)=f(x)+g(x)在区间[-2,2]上的最大值.
| 2 |
(Ⅱ)根据f(x)和g(x)的函数解析式,分类表示出F(x)的解析式,写成分段函数,再根据分段函数的解析式,即可求出F(x)在(-∞,0)上的最小值;
(Ⅲ)根据f(x)和g(x)的函数解析式,求出G(x)的解析式,再分别针对每一段上的解析式分别求解最值,在对每一段中的最值进行分类比较,确定其中的最大值,即可求得函数G(x)=f(x)+g(x)在区间[-2,2]上的最大值.
解答:解:(Ⅰ)∵f(x)=|x2-1|,
∴f(x)=
,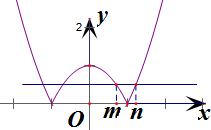
作出f(x)的图象,由f(x)的图象可知,0≤m<1<n≤
,
∵f(m)=f(n),
∴1-m2=n2-1,
∴m2+n2=2;
(Ⅱ)∵x<0,
∴f(x)=
,
∵k=
,
∴g(x)=
-
x,x∈(-∞,0),
当x≤-1时,f(x)≥g(x),即为x2-1≥
-
x,解得x≤-
,
当-1<x<0时,f(x)≥g(x),即为1-x2≥
-
x,解得-
≤x<0,
∴F(x)=
,
①当x≤-
时,F(x)=x2-1,
∵F(x)在(-∞,-
]上单调递减,
∴F(x)的最小值为F(-
)=
;
②当-
<x<-
时,F(x)=
-
x,
∵F(x)在(-
,-
)上单调递减,
∴F(x)<F(-
),
∴F(x)<
;
③当-
≤x<0时,F(x)=1-x2,
∵F(x)在(-
,0)上单调递增,
∴F(x)的最小值为F(-
)=
.
综合①②③可得,当x=-
时,F(x)的最小值为
;
∴当k=
时,F(x)在(-∞,0)上的最小值为
;
(Ⅲ)∵G(x)=f(x)+g(x),且f(x)=|x2-1|,g(x)=k|x-1|,
∴G(x)═
,
①记G1(x)=x2+kx-k-1,x∈[1,2],
对称轴为x=-
,根据对称轴与区间的位置关系可得,
当-
≤
,即k≥-3时,G1(x)max=G1(2)=k+3,
当-
>
,即k<-3时,G1(x)max=G1(1)=0,
②记G2(x)=-x2-kx+k+1,x∈[-1,1],
对称轴为x=-
,根据对称轴与区间的位置关系可得,
当-
≤-1,即k≥2时,G2(x)max=G2(-1)=2k,
当-1<-
<1,即-2<k<2时,G2(x)max=G2(-
)=(
+1)2,
当-
≥1,即k≤-2时,G2(x)max=G2(1)=0,
③记G(x)=x2-kx+k-1,x∈[-2,-1],
对称轴为x=
,根据对称轴与区间的位置关系可得,
当
≥-
,即k≥-3时,G3(x)max=G3(-2)=3k+3,
当
<-
,即k<-时,G3(x)max=G3(-1)=2k,
由上讨论可知,
当k<-3时,G(x)max=max{0,2k}=0,
当-3≤k≤-2时,G(x)max=max{k+3,0,3k+3}=k+3,
当-2<k<0时,G(x)max=max{k+3,(
+1)2,3k+3}=k+3,
当0≤k<2时,G(x)max=max{k+3,(
+1)2,3k+3}=3k+3,
当k≥2时,G(x)max=max{k+3,2k,3k+3}=3k+3,
综上所述:当k<-3时,G(x)在[-2,2]上的最大值为0,
当-3≤k<0时,G(x)在[-2,2]上的最大值为k+3,
当k≥0时,G(x)在[-2,2]上的最大值为3k+3.
∴f(x)=
|

作出f(x)的图象,由f(x)的图象可知,0≤m<1<n≤
| 2 |
∵f(m)=f(n),
∴1-m2=n2-1,
∴m2+n2=2;
(Ⅱ)∵x<0,
∴f(x)=
|
∵k=
| 1 |
| 2 |
∴g(x)=
| 1 |
| 2 |
| 1 |
| 2 |
当x≤-1时,f(x)≥g(x),即为x2-1≥
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
当-1<x<0时,f(x)≥g(x),即为1-x2≥
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴F(x)=
|
①当x≤-
| 3 |
| 2 |
∵F(x)在(-∞,-
| 3 |
| 2 |
∴F(x)的最小值为F(-
| 3 |
| 2 |
| 5 |
| 4 |
②当-
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵F(x)在(-
| 3 |
| 2 |
| 1 |
| 2 |
∴F(x)<F(-
| 1 |
| 2 |
∴F(x)<
| 3 |
| 4 |
③当-
| 1 |
| 2 |
∵F(x)在(-
| 1 |
| 2 |
∴F(x)的最小值为F(-
| 1 |
| 2 |
| 3 |
| 4 |
综合①②③可得,当x=-
| 1 |
| 2 |
| 3 |
| 4 |
∴当k=
| 1 |
| 2 |
| 3 |
| 4 |
(Ⅲ)∵G(x)=f(x)+g(x),且f(x)=|x2-1|,g(x)=k|x-1|,
∴G(x)═
|
①记G1(x)=x2+kx-k-1,x∈[1,2],
对称轴为x=-
| k |
| 2 |
当-
| k |
| 2 |
| 3 |
| 2 |
当-
| k |
| 2 |
| 3 |
| 2 |
②记G2(x)=-x2-kx+k+1,x∈[-1,1],
对称轴为x=-
| k |
| 2 |
当-
| k |
| 2 |
当-1<-
| k |
| 2 |
| k |
| 2 |
| k |
| 2 |
当-
| k |
| 2 |
③记G(x)=x2-kx+k-1,x∈[-2,-1],
对称轴为x=
| k |
| 2 |
当
| k |
| 2 |
| 3 |
| 2 |
当
| k |
| 2 |
| 3 |
| 2 |
由上讨论可知,
当k<-3时,G(x)max=max{0,2k}=0,
当-3≤k≤-2时,G(x)max=max{k+3,0,3k+3}=k+3,
当-2<k<0时,G(x)max=max{k+3,(
| k |
| 2 |
当0≤k<2时,G(x)max=max{k+3,(
| k |
| 2 |
当k≥2时,G(x)max=max{k+3,2k,3k+3}=3k+3,
综上所述:当k<-3时,G(x)在[-2,2]上的最大值为0,
当-3≤k<0时,G(x)在[-2,2]上的最大值为k+3,
当k≥0时,G(x)在[-2,2]上的最大值为3k+3.
点评:本题考查了分段函数的图象,分段函数的最值.对于含有绝对值的函数,通常转化为分段函数来解答,对于分段函数的问题,一般选用分类讨论和数形结合的思想方法进行求解.本题综合应用了分类讨论和数形结合的数学思想方法.属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|