题目内容

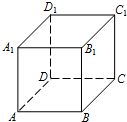在直四棱柱ABCD-A1B1C1D1中，底面是有一个角为60°的菱形，AA1=AB，从顶点中取出三个能构成不同直角三角形的个数有（　　）个．
分析：由题意可得，这3个顶点必须在直四棱柱的4个侧面内，或在2个互相垂直的对角面ACC1A1和 BDD1B1内，故有6C43 个．
解答：解：在直四棱柱ABCD-A1B1C1D1中，底面是有一个角为60°的菱形，AA1=AB，
故在直四棱柱ABCD-A1B1C1D1的4个侧面都是正方形，对角面ACC1A1和 BDD1B1 中一个是矩形，另一个是正方形．
直四棱柱的上下底面和其它的对角面不是矩形．
而每个正方形的4个顶点中任意三点的连线都构成直角三角形，共有5C43=20个．
矩形的4个顶点中任意取3个点的连线也都构成直角三角形，共有C43=4个．
根据分类计数原理，构成不同直角三角形的个数有 5C43+C43=24个，
故选：C．
点评：本题主要考组合及两个基本原理，组合数公式的应用，体现了分类讨论的数学思想．
练习册系列答案
相关题目
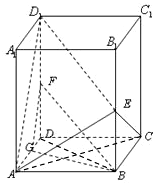精英家教网在直四棱柱ABCD-A1B1C1D1中，AA1=2，底面是边长为1的正方形，E、G、F分别是棱B1B、D1D、DA的中点．
（Ⅰ）求证：平面AD1E∥平面BGF；
（Ⅱ）求证：D1E⊥平面AEC．
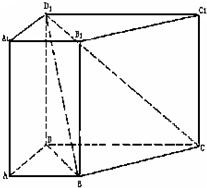精英家教网在直四棱柱ABCD-A1B1C1D1中，已知AB∥CD，AB=AD=1，D1D=CD=2，AB⊥AD．
（I）求证：BC⊥面D1DB；
（II）求D1B与平面D1DCC1所成角的大小；
（III）在BB1上是否存在一点F，使F到平面D1BC的距离为
3
3
，若存在，则指出该点的位置；若不存在，请说明理由．
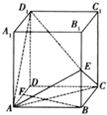精英家教网在直四棱柱ABCD-A1B1C1D1中，AA1=2，底面是边长为1的正方形，E、F分别是棱B1B、DA的中点．
（1）求证：BF∥平面AD1E；
（2）求证：D1E⊥平面AEC．
如图，在直四棱柱ABCD-A1B1C1D1中，点E，F分别在AA1，CC1上，且AE=
3
4
AA1，CF=
1
3
CC1，点A，C到BD的距离之比为3：2，则三棱锥E-BCD和F-ABD的体积比
VE-BCD
VF-ABD
=
3
2
3
2
．
在直四棱柱ABCD-A1B1C1D1中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，AB=AD=1，CD=CC1=2，E为棱AA1的中点，F为棱BB1上的动点．
（Ⅰ）试确定点F的位置，使得D1E⊥DF；
（Ⅱ）在（Ⅰ）的条件下，求CF与平面EFD1所成角的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网