题目内容
在△ABC中,若cosA=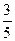 ,cosB=
,cosB=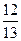 , 试判断三角形的形状.
, 试判断三角形的形状.
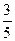 ,cosB=
,cosB=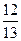 , 试判断三角形的形状.
, 试判断三角形的形状.△ABC为钝角三角形
∵在△ABC中,若cosA=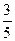 >0 ,cosB=
>0 ,cosB=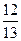 >0 ∴A,B为锐角
>0 ∴A,B为锐角
sinA=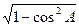 =
=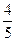 sinB=
sinB=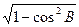 =
=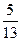
∵ cosC=cos[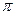 -(A+B)]=-cos(A+B)=-(cosAcosB-sinAsinB)=
-(A+B)]=-cos(A+B)=-(cosAcosB-sinAsinB)=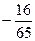 < 0
< 0
∴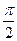 < C <
< C <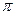 即C为钝角
即C为钝角
∴△ABC为钝角三角形.
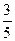 >0 ,cosB=
>0 ,cosB=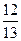 >0 ∴A,B为锐角
>0 ∴A,B为锐角sinA=
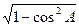 =
=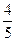 sinB=
sinB=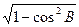 =
=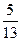
∵ cosC=cos[
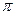 -(A+B)]=-cos(A+B)=-(cosAcosB-sinAsinB)=
-(A+B)]=-cos(A+B)=-(cosAcosB-sinAsinB)=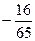 < 0
< 0∴
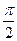 < C <
< C <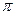 即C为钝角
即C为钝角∴△ABC为钝角三角形.

练习册系列答案
相关题目
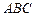 中,内角
中,内角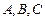 的对边分别是
的对边分别是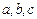 ,已知
,已知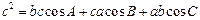 .
.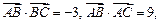 求角B的大小.
求角B的大小.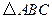 中,已知
中,已知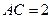 ,
,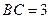 ,
,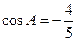 .
. 的值;(Ⅱ)求
的值;(Ⅱ)求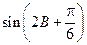 的值
的值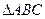 中,角
中,角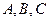 所对的边分别为
所对的边分别为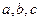 ,且
,且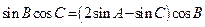 .
.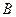 的大小;
的大小;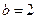 ,
,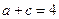 ,求
,求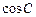 ;
;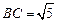 ,求
,求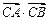 的值
的值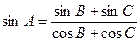 ,判断△ABC的形状.
,判断△ABC的形状. ,求△POC面积的最大值及此时
,求△POC面积的最大值及此时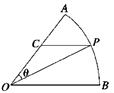
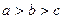 且
且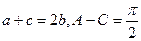 ,求
,求