题目内容
(本小题满分12分)
在四棱柱 中,底面
中,底面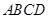 是直角梯形,AB∥CD,∠ABC=
是直角梯形,AB∥CD,∠ABC=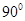 ,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD
,AB=PB=PC=BC=2CD=2,平面PBC⊥平面ABCD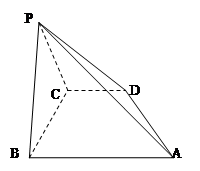
(1)求证:AB⊥平面PBC
(2)求三棱锥C-ADP的体积
(3)在棱PB上是否存在点M使CM∥平面PAD?
若存在,求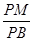 的值。若不存在,请说明理由。
的值。若不存在,请说明理由。
(1)证明:因为∠ABC=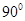 ,所以AB⊥BC。因为平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,AB
,所以AB⊥BC。因为平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC,AB 平面ABCD,所以AB⊥平面PBC ;(2)
平面ABCD,所以AB⊥平面PBC ;(2)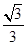 ;(3)在棱PB上存在点M使得CM∥平面PAD,此时
;(3)在棱PB上存在点M使得CM∥平面PAD,此时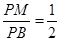
解析试题分析:(1)证明:因为∠ABC=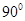 ,所以AB⊥BC。 (1分)
,所以AB⊥BC。 (1分)
因为平面PBC⊥平面ABCD,平面PBC∩平面ABCD=BC
AB 平面ABCD,所以AB⊥平面PBC (4分)
平面ABCD,所以AB⊥平面PBC (4分)
(2)取BC的中点O,连接PO
因为PB=PC,所以PO⊥BC
因为平面PBC⊥平面ABCD
平面PBC∩平面ABCD=BC,PO 平面PBC
平面PBC
所以PO⊥平面ABCD (5分) 在等边△PBC中PO=
在等边△PBC中PO=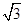

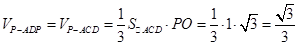 (8分)
(8分)
(3)在棱PB上存在点M使得CM∥平面PAD,此时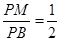
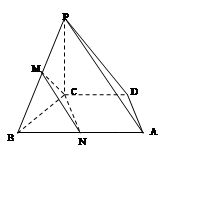 证明:取AB的中点N,连接CM,CN,MN
证明:取AB的中点N,连接CM,CN,MN
则MN∥PA,AN=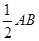
因为AB ="2CD" 所以AN=CD
因为AB ∥CD所以四边形ANCD是平行四边形。
所以CN∥AD
因为MN∩CN=N,PA∩AD=A
所以平面MNC∥平面PAD (10分)
因为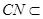 平面MNC
平面MNC
所以CM∥平面PAD ( 12分)
考点:本题考查了空间中的线面关系
点评:以棱锥柱为载体考查立体几何中的线面、面面、点面位置关系或距离是高考的亮点,掌握其判定性质及定理,是解决此类问题的关键

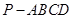 中
中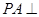 平面
平面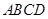 ,
,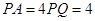 ,底面为直角梯形,
,底面为直角梯形,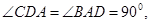
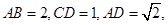
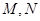 分别是
分别是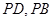 的中点.
的中点.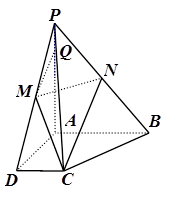
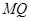 // 平面
// 平面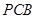 ;
;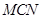 与底面
与底面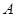 到平面
到平面
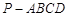 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形,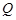 是棱
是棱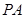 上的动点.
上的动点.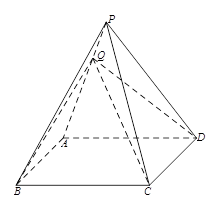
 是
是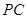 //平面
//平面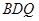 ;
;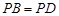 ,求证:
,求证: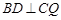 ;
;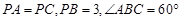 ,求四棱锥
,求四棱锥
 中,底面ABCD是一直角梯形,
中,底面ABCD是一直角梯形,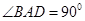 ,
,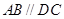 ,
, ,且PA=AD=DC=
,且PA=AD=DC=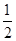 AB=1.
AB=1.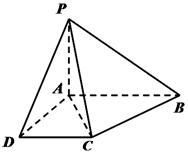
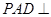 平面
平面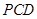
 与
与 所成角的余弦值
所成角的余弦值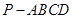 中,
中,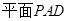
 平面
平面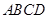 ,底面
,底面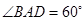 .
.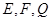 分别是
分别是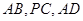 的中点.
的中点.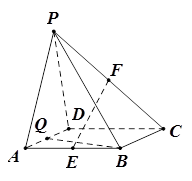
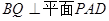 ;
;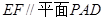 .
.