题目内容
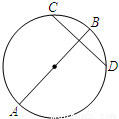
 如图,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P.若PD=
如图,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P.若PD=| 2a | 3 |
分析:利用垂径定理及其相交弦定理即可得出.
解答:解:①∵OP⊥AB,∴AP=PB.
在Rt△OAP中,∵∠OAP=30°,OA=a,∴AP=acos30°=
a,∴AB=
a.
②由相交弦定理可得:CP•PD=AP•PB,∴CP=
=
.
故答案分别为
a,
.
在Rt△OAP中,∵∠OAP=30°,OA=a,∴AP=acos30°=
| ||
| 2 |
| 3 |
②由相交弦定理可得:CP•PD=AP•PB,∴CP=
(
| ||||
|
| 9a |
| 8 |
故答案分别为
| 3 |
| 9a |
| 8 |
点评:熟练掌握圆的垂径定理及其相交弦定理是解题的关键.

练习册系列答案
相关题目
 (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题) ,求线段AC的长度.
,求线段AC的长度. 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程. (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
 ,求线段AC的长度.
,求线段AC的长度. 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程. (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
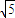 ,求线段AC的长度.
,求线段AC的长度. 的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.
的一个特征值是3,求直线x-2y-3=0在M作用下的新直线方程.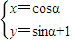 (α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.
(α是参数),若以O为极点,x轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线C的极坐标方程.