题目内容
已知变量t,y满足关系式loga
=logt
,a>0且a≠1,t>0且t≠1,变量t,x满足关系式t=ax,变量y,x满足函数关系式y=f(x).
(1)求函数y=f(x)表达式;
(2)若函数y=f(x)在[2a,3a]上具有单调性,求实数a的取值范围.
| t |
| a3 |
| y |
| a3 |
(1)求函数y=f(x)表达式;
(2)若函数y=f(x)在[2a,3a]上具有单调性,求实数a的取值范围.
分析:(1)把t=ax代入loga
=logt
中,利用对数恒等式化简得x-3=logt
,利用对数和指数的互化以及指数的运算性质,即可求得y=f(x)的表达式.
(2)f(x)=ax2-3x+3((x≠0)=a(x-
)2+
(x≠0),由f(x)在[2a,3a]上具有单调性,得3a≤
或2a≥
,解出即可;
| t |
| a3 |
| y |
| a3 |
| y |
| a3 |
(2)f(x)=ax2-3x+3((x≠0)=a(x-
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:(1)由loga
=logt
,得logat-logaa3=logt
,
又t=ax,∴logaax-3=logt
,即x-3=logt
,
∴
=tx-3=(ax)x-3=ax2-3x,
∴y=a3ax2-3x=ax2-3x+3(x≠0),
故y=f(x)=ax2-3x+3(x≠0);
(2)∵f(x)=ax2-3x+3(x≠0)=a(x-
)2+
(x≠0),且f(x)在[2a,3a]上具有单调性,
∴3a≤
或2a≥
,解得a≤
或a≥
且a≠1,
故实数a的取值范围是:(0,
]∪[
,1)∪(1,+∞).
| t |
| a3 |
| y |
| a3 |
| y |
| a3 |
又t=ax,∴logaax-3=logt
| y |
| a3 |
| y |
| a3 |
∴
| y |
| a3 |
∴y=a3ax2-3x=ax2-3x+3(x≠0),
故y=f(x)=ax2-3x+3(x≠0);
(2)∵f(x)=ax2-3x+3(x≠0)=a(x-
| 3 |
| 2 |
| 3 |
| 4 |
∴3a≤
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
故实数a的取值范围是:(0,
| 1 |
| 2 |
| 3 |
| 4 |
点评:本题考查对数的运算法则和指数与对数的互化、复合函数的单调性等基础知识,注意函数的定义域,考查了运算能力.

练习册系列答案
相关题目
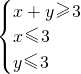 ,z=x2+(y+1)2,则z的最大值是________.
,z=x2+(y+1)2,则z的最大值是________.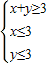 ,z=x2+(y+1)2,则z的最大值是 .
,z=x2+(y+1)2,则z的最大值是 .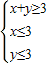 ,z=x2+(y+1)2,则z的最大值是 .
,z=x2+(y+1)2,则z的最大值是 .