题目内容
 已知函数f(x)=|x-1|.
已知函数f(x)=|x-1|.(1)用分段函数的形式表示该函数;
(2)在右边所给的坐标第中画出该函数的图象;
(3)写出该函数的定义域、值域、奇偶性、单调区间(不要求证明).
分析:(1)根据绝对值的意义,分当x≥1时,当x<1时两种情况求解,最后再写成分段函数的形式,
(2)每一段都是一次函数,图象是一条直线,在定义域内任取两点作图即可.
(3)根据图象,定义域即看横轴覆盖部分,值域即看纵轴覆盖部分,奇偶性,看是否关于原点对称或关于纵轴对称.单调增区间看上升趋势,单调减区间看下降趋势.
(2)每一段都是一次函数,图象是一条直线,在定义域内任取两点作图即可.
(3)根据图象,定义域即看横轴覆盖部分,值域即看纵轴覆盖部分,奇偶性,看是否关于原点对称或关于纵轴对称.单调增区间看上升趋势,单调减区间看下降趋势.
解答:解:(1)y=
(2)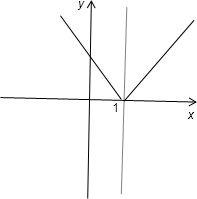
(3)定义域为R,值域为{y|y≥0},图象即不关于原点对称也不关于y轴对称,所以f(x)是非奇非偶函数,
单调增区间[1,+∞),单调减区间(-∞,1)
|
(2)

(3)定义域为R,值域为{y|y≥0},图象即不关于原点对称也不关于y轴对称,所以f(x)是非奇非偶函数,
单调增区间[1,+∞),单调减区间(-∞,1)
点评:本题主要考查绝对值函数转化为分段函数,研究其图象和性质.还考查了数形结合的思想与方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|