题目内容
当x∈R时,函数y=f(x)满足:f(1.1+x)+f(3.1+x)=f(2.1+x),且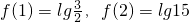 ,,则f(2012)=
,,则f(2012)=
- A.lg2
- B.-lg2
- C.lg15
- D.-lg15
C
分析:依次将0.1、0.9、1.9、2.9、3.9、4.9代入可知函数f(x)是以6为周期的周期函数,f又(2012)=f(335×6+2)=f(2)=lg15
从而可得答案.
解答:令x=-0.1,代入得 f(1)+f(3)=f(2),∴f(3)=f(2)-f(1)=lg15-lg =1
=1
令x=0.9,代入得 f(2)+f(4)=f(3),∴f(4)=f(3)-f(2)=1-lg15=lg
令x=1.9,代入得 f(3)+f(5)=f(4),∴f(5)=f(4)-f(3)=-lg15
令x=2.9,代入得 f(4)+f(6)=f(5),∴f(6)=f(5)-f(4)=-1
令x=3.9,代入得 f(5)+f(7)=f(6),∴f(7)=f(6)-f(5)=lg =f(1)
=f(1)
令x=4.9,代入得 f(6)+f(8)=f(7),∴f(8)=f(7)-f(6)=lg15=f(2)
由上可得函数f(x)是以6为周期的周期函数
f(2003)=f(335×6+2)=f(2)=lg15
故选C.
点评:本题主要考查函数的基本性质--周期性.这种题型主要就在于找规律,发现周期,一般情况多代入几个数就可以发现规律.
分析:依次将0.1、0.9、1.9、2.9、3.9、4.9代入可知函数f(x)是以6为周期的周期函数,f又(2012)=f(335×6+2)=f(2)=lg15
从而可得答案.
解答:令x=-0.1,代入得 f(1)+f(3)=f(2),∴f(3)=f(2)-f(1)=lg15-lg
 =1
=1令x=0.9,代入得 f(2)+f(4)=f(3),∴f(4)=f(3)-f(2)=1-lg15=lg

令x=1.9,代入得 f(3)+f(5)=f(4),∴f(5)=f(4)-f(3)=-lg15
令x=2.9,代入得 f(4)+f(6)=f(5),∴f(6)=f(5)-f(4)=-1
令x=3.9,代入得 f(5)+f(7)=f(6),∴f(7)=f(6)-f(5)=lg
 =f(1)
=f(1)令x=4.9,代入得 f(6)+f(8)=f(7),∴f(8)=f(7)-f(6)=lg15=f(2)
由上可得函数f(x)是以6为周期的周期函数
f(2003)=f(335×6+2)=f(2)=lg15
故选C.
点评:本题主要考查函数的基本性质--周期性.这种题型主要就在于找规律,发现周期,一般情况多代入几个数就可以发现规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
当x∈R时,函数y=f(x)满足:f(1.1+x)+f(3.1+x)=f(2.1+x),且f(1)=lg
,f(2)=lg15,则f(2003)=( )
| 3 |
| 2 |
| A、lg2 | B、-lg2 |
| C、lg15 | D、-lg15 |
当x∈R时,函数y=f(x)满足:f(1.1+x)+f(3.1+x)=f(2.1+x),且f(1)=lg
,f(2)=lg15,则f(2012)=( )
| 3 |
| 2 |
| A、lg2 | B、-lg2 |
| C、lg15 | D、-lg15 |
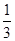 ,且f(1)=1,则f(100)
,且f(1)=1,则f(100)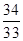 B.
B.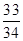 C.34 D.
C.34 D.