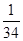题目内容
当x∈R时,函数y=sinx-
cosx的值域是
| 3 |
[-2,2]
[-2,2]
.分析:函数解析式提取2变形后,利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域求出y的值域即可.
解答:解:y=sinx-
cosx=2(
sinx-
cosx)=2sin(x-
),
∵-1≤sin(x-
)≤1,即-2≤2sin(x-
)≤2,
则y=sinx-
cosx的值域是[-2,2].
故答案为:[-2,2]
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∵-1≤sin(x-
| π |
| 3 |
| π |
| 3 |
则y=sinx-
| 3 |
故答案为:[-2,2]
点评:此题考查了两角和与差的正弦函数公式,以及正弦函数的定义域与值域,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
当x∈R时,函数y=f(x)满足:f(1.1+x)+f(3.1+x)=f(2.1+x),且f(1)=lg
,f(2)=lg15,则f(2003)=( )
| 3 |
| 2 |
| A、lg2 | B、-lg2 |
| C、lg15 | D、-lg15 |
当x∈R时,函数y=f(x)满足:f(1.1+x)+f(3.1+x)=f(2.1+x),且f(1)=lg
,f(2)=lg15,则f(2012)=( )
| 3 |
| 2 |
| A、lg2 | B、-lg2 |
| C、lg15 | D、-lg15 |
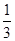 ,且f(1)=1,则f(100)
,且f(1)=1,则f(100)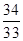 B.
B.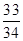 C.34 D.
C.34 D.