题目内容
(08年鄞州中学模拟理)(14分)如图四棱锥P―ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,![]() ,BG⊥GC,GB=GC=2,E是BC的中点.
,BG⊥GC,GB=GC=2,E是BC的中点.
(1)求异面直线GE与PC所成的角;
(2)求点D到平面PBG的距离;
(3)若F点是棱PC上一点,且DF⊥GC,求![]() 的值.
的值.

解析:(1)解:以G点为原点,![]() 为x轴、y轴、z轴建立空间直角坐标系,
为x轴、y轴、z轴建立空间直角坐标系,
则B(2,0,0),C(0,2,0),P(0,0,4), 故E(1,1,0) ![]() =(1,1,0),
=(1,1,0),
![]() =(0,2,4)
=(0,2,4) ![]()
∴GE与PC所成的角为arccos![]() .………………5分
.………………5分
(2)解:平面PBG的单位法向量n=(0,±1,0) ∵![]()
∴点D到平面PBG的距离为![]() n |=
n |=![]() .......................9分
.......................9分
(3)解:设F(0,y,z),则![]()
∵![]() ,∴
,∴![]() , 即
, 即![]() ,∴
,∴![]()
又![]() ,即(0,
,即(0,![]() ,z-4)=λ(0,2,-4),∴z=1,
,z-4)=λ(0,2,-4),∴z=1,
故F(0,![]() ,1)
,1) ![]() ,∴
,∴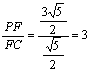 .......14分
.......14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
