题目内容
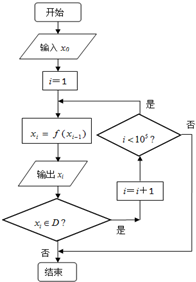请认真阅读下列程序框图：已知程序框图中的函数关系式为f(x)=| 4x-2 |
| x+1 |
（1）输入x0=
| 49 |
| 65 |
（2）若输入一个正数x0时，产生的数列{xn}满足：任意一项xn，都有xn＜xn+1，试求正数x0的取值范围．
分析：（1）利用f(x)=
，x0=
及程序框图，注意函数的定义域，直接可求得数列{xn}的只有三项；
（3）要使对任意正整数n，均有xn＜xn+1，则必须
＞xn，得1＜xn＜2，要使任意一项xn，都有xn+1＞xn，须（x0-2）（x0-1）＜0，解得：1＜x0＜2，从而得出结论．
| 4x-2 |
| x+1 |
| 49 |
| 65 |
（3）要使对任意正整数n，均有xn＜xn+1，则必须
| 4xn-2 |
| xn+1 |
解答：解：（1）当x0=
时，
x1=f(
)=
，x2=f(
)=
，x3=f(
)=-1
所以输出的数列为
，
，-1
（2）由题意知 xn+1=f(xn)=
＞xn，
因为x0＞0，∴xn＞0，有：
＞xn
得4xn-2＞xn（xn+1）
即xn2-3xn+2＜0，即（xn-2）（xn-1）＜0
要使任意一项xn，都有xn+1＞xn，
须满足（x0-2）（x0-1）＜0，解得：1＜x0＜2，
所以当正数x0在（1，2）内取值时，所输出的数列{xn}对任意正整数n满足xn＜xn+1．
| 49 |
| 65 |
x1=f(
| 49 |
| 65 |
| 11 |
| 19 |
| 11 |
| 19 |
| 1 |
| 5 |
| 1 |
| 5 |
所以输出的数列为
| 11 |
| 19 |
| 1 |
| 5 |
（2）由题意知 xn+1=f(xn)=
| 4xn-2 |
| xn+1 |
因为x0＞0，∴xn＞0，有：
| 4xn-2 |
| xn+1 |
得4xn-2＞xn（xn+1）
即xn2-3xn+2＜0，即（xn-2）（xn-1）＜0
要使任意一项xn，都有xn+1＞xn，
须满足（x0-2）（x0-1）＜0，解得：1＜x0＜2，
所以当正数x0在（1，2）内取值时，所输出的数列{xn}对任意正整数n满足xn＜xn+1．
点评：本小题主要考查数列与算法的简单结合、不等式的解法等基础知识，考查运算求解能力，考查化归与转化思想．属于中档题．
练习册系列答案
相关题目
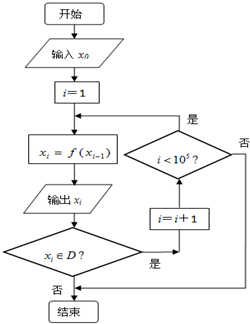
请认真阅读下列程序框图：
请认真阅读下列程序框图：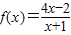
，程序框图中的D为函数f（x）的定义域，把此程序框图中所输出的数xi组成一个数列{xn}．
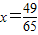，请写出数列{xn}的所有项；
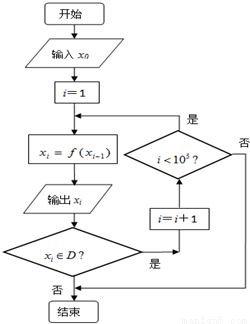请认真阅读下列程序框图：
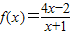，程序框图中的D为函数f（x）的定义域，把此程序框图中所输出的数xi组成一个数列{xn}．
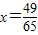，请写出数列{xn}的所有项；