题目内容
已知函数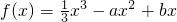 .(a,b∈R)
.(a,b∈R)
( I)若f'(0)=f'(2)=1,求函数f(x)的解析式;
( II)若b=a+2,且f(x)在区间(0,1)上单调递增,求实数a的取值范围.
解:(Ⅰ)因为f'(x)=x2-2ax+b,
由f'(0)=f'(2)=1即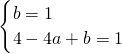 得
得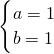 ,
,
所以f(x)的解析式为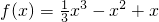 .
.
(Ⅱ)若b=a+2,则f'(x)=x2-2ax+a+2,△=4a2-4(a+2),
(1)当△≤0,即-1≤a≤2时,f'(x)≥0恒成立,那么f(x)在R上单调递增,
所以,当-1≤a≤2时,f(x)在区间(0,1)上单调递增;
(2)当△>0,即a>2或a<-1时,
因为f'(x)=x2-2ax+a+2的对称轴方程为x=a
要使函数f(x)在区间(0,1)上单调递增,
需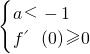 或
或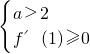
解得-2≤a<-1或2<a≤3.
综上:当a∈[-2,3]时,函数f(x)在区间(0,1)上单调递增.
分析:(Ⅰ)先求出函数的导数,再根据f'(0)=f'(2)=1,就可求出a,b的值,代入函数解析式即可.
( II)把b=a+2代入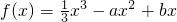 ,使函数中只含参数a,因为f(x)在区间(0,1)上单调递增,所以区间(0,1)是函数增区间的一个子区间,而函数
,使函数中只含参数a,因为f(x)在区间(0,1)上单调递增,所以区间(0,1)是函数增区间的一个子区间,而函数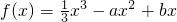 是二次函数,开口向上,所以在对称轴右侧为增函数,所以只要(0,1)位于函数对称轴右侧即可.
是二次函数,开口向上,所以在对称轴右侧为增函数,所以只要(0,1)位于函数对称轴右侧即可.
点评:本题考查了导数的求法,以及函数单调性的判断,做题时要细心.
由f'(0)=f'(2)=1即
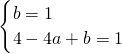 得
得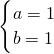 ,
,所以f(x)的解析式为
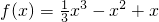 .
.(Ⅱ)若b=a+2,则f'(x)=x2-2ax+a+2,△=4a2-4(a+2),
(1)当△≤0,即-1≤a≤2时,f'(x)≥0恒成立,那么f(x)在R上单调递增,
所以,当-1≤a≤2时,f(x)在区间(0,1)上单调递增;
(2)当△>0,即a>2或a<-1时,
因为f'(x)=x2-2ax+a+2的对称轴方程为x=a
要使函数f(x)在区间(0,1)上单调递增,
需
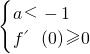 或
或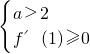
解得-2≤a<-1或2<a≤3.
综上:当a∈[-2,3]时,函数f(x)在区间(0,1)上单调递增.
分析:(Ⅰ)先求出函数的导数,再根据f'(0)=f'(2)=1,就可求出a,b的值,代入函数解析式即可.
( II)把b=a+2代入
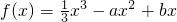 ,使函数中只含参数a,因为f(x)在区间(0,1)上单调递增,所以区间(0,1)是函数增区间的一个子区间,而函数
,使函数中只含参数a,因为f(x)在区间(0,1)上单调递增,所以区间(0,1)是函数增区间的一个子区间,而函数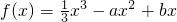 是二次函数,开口向上,所以在对称轴右侧为增函数,所以只要(0,1)位于函数对称轴右侧即可.
是二次函数,开口向上,所以在对称轴右侧为增函数,所以只要(0,1)位于函数对称轴右侧即可.点评:本题考查了导数的求法,以及函数单调性的判断,做题时要细心.

练习册系列答案
相关题目
 已知函数
已知函数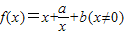 ,其中a,b∈R.
,其中a,b∈R.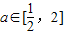 ,不等式f(x)≤10在
,不等式f(x)≤10在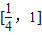 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.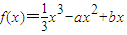 .(a,b∈R)
.(a,b∈R) ,其中a,b∈R.
,其中a,b∈R. ,不等式f(x)≤10在
,不等式f(x)≤10在 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.