题目内容
(文)一个口袋装有大小相同的2个白球和3个黑球,从中摸出2个球.
求:(Ⅰ)两个球恰好颜色相同的概率;
(Ⅱ)两个球恰好颜色不同的概率.
(理)已知10件产品中有3件是次品.
(Ⅰ)任意取出3件产品作检验,求其中至少有1件是次品的概率;
(Ⅱ)为了保证使3件次品全部检验出的概率超过0.6,最少应抽取几件产品作检验?
【答案】
(Ⅱ)两球恰好颜色不同的概率为:P2
=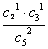 =
=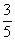 =0.6………………………12分
=0.6………………………12分
(文)解:(Ⅰ)两球恰好颜色相同的概率为:P1 =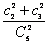 =
=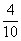 =
=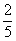 (或0.4)………6分
(或0.4)………6分
|
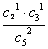 =
=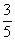 =0.6………………………12分
=0.6………………………12分
(理)解:(Ⅰ)任意取出3件产品作检验,全部是正品的概率为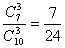 ……3分
……3分
至少有一件是次品的概率为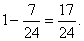 ……………………6分
……………………6分
(Ⅱ)设抽取n件产品作检验,则3件次品全部检验出的概率为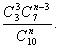 …8分
…8分
由
整理得: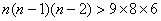 ,……………………10分
,……………………10分
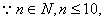 ∴当n=9或n=10时上式成立.…………11分
∴当n=9或n=10时上式成立.…………11分
答:任意取出3件产品作检验,其中至少有1件是次品的概率为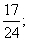 为了保证使3件次品全部检验出的概率超过0.6,最少应抽取9件产品作检验.………………12分
为了保证使3件次品全部检验出的概率超过0.6,最少应抽取9件产品作检验.………………12分

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目