题目内容
若M(3,-1),N(0,1)是一次函数f(x)图象上的两点,那么|f(x+1)|<1的解集是
- A.(1,4)
- B.(-1,2)
- C.(-∞,-1)∪(4,+∞)
- D.(-∞,-1)∪(2,+∞)
B
分析:依题意可求得一次函数f(x)的方程,从而可得f(x+1)的表达式,解不等式|f(x+1)|<1即可.
解答:依题意,直线MN的斜率k=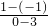 =-
=- ,
,
∴直线MN的方程为:y-1=- x,
x,
∴y=- x+1,即f(x)=-
x+1,即f(x)=- x+1,
x+1,
∴f(x+1)=- (x+1)+1=
(x+1)+1= ,
,
∴由|f(x+1)|<1得:| |<1,
|<1,
∴-1<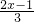 <1,解得-1<x<2.
<1,解得-1<x<2.
∴|f(x+1)|<1的解集是(-1,2).
故选B.
点评:本题考查绝对值不等式的解法,考查直线的方程,求得一次函数f(x)的方程是关键,属于中档题.
分析:依题意可求得一次函数f(x)的方程,从而可得f(x+1)的表达式,解不等式|f(x+1)|<1即可.
解答:依题意,直线MN的斜率k=
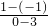 =-
=- ,
,∴直线MN的方程为:y-1=-
 x,
x,∴y=-
 x+1,即f(x)=-
x+1,即f(x)=- x+1,
x+1,∴f(x+1)=-
 (x+1)+1=
(x+1)+1= ,
,∴由|f(x+1)|<1得:|
 |<1,
|<1,∴-1<
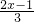 <1,解得-1<x<2.
<1,解得-1<x<2.∴|f(x+1)|<1的解集是(-1,2).
故选B.
点评:本题考查绝对值不等式的解法,考查直线的方程,求得一次函数f(x)的方程是关键,属于中档题.

练习册系列答案
相关题目
已知a,b,c为△ABC的三个内角A,B,C的对边,向量
=(
,-1),
=(cosA,sinA).若
⊥
,且αcosB+bcosA=csinC,则角A,B的大小分别为( )
| m |
| 3 |
| n |
| m |
| n |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|