Question

【题目】已知椭圆的两个焦点为，，离心率.

（1）求椭圆的方程；

（2）设直线与椭圆交于，两点，线段的垂直平分线交轴于点，当变化时，求面积的最大值.

Answer 1

【答案】（1）；（2）

【解析】试题分析：（1）根据椭圆几何条件得，再由离心率解得，即得，（2）由直线与椭圆有两个交点得判别式大于零，解得m取值范围，再根据点斜式写出线段的垂直平分线方程，解得点坐标，根据点到直线距离公式得高，根据弦长公式得底边边长，根据三角形面积公式得面积函数关系式，最后根据二次函数性质求最大值.

试题解析：（1）由离心率，半焦距，解得.

所以，所以椭圆的方程是.

（2）解：设，，

据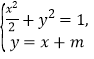得

∵直线与椭圆有两个不同的交点，

∴，又，所以且.

由根与系数的关系得，

设线段中点为，点横坐标，，∴，

∴线段垂直平分线方程为，∴点坐标为，

点到直线的距离，

又，

所以

，所以当时，三角形面积最大，且.