题目内容
已知集合A={1，2，3}，B={4，5，6}，从A到B的映射f（x），B中有且仅有2个元素有原象，则这样的映射个数为（ ）A．8
B．18
C．24
D．27
【答案】分析：从A中3个元素中选出2个元素，使者两个元素的像相同，有c32=3种方法； 再从B中3个元素中找出2和元素作像，有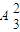
=6种方法，利用乘法原理求的结果．
解答：解：由题意可得，A中3个元素中只有2个元素的像相同，
从A中3个元素中选出2个元素，使者两个元素的像相同，有c32=3种方法．
再从B中3个元素中找出2和元素作像，有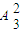
=6种方法．
根据分步计数原理，这样的映射个数为 3×6=18个，
故选B
点评：本题考查映射的概念，分步计数原理的应用，属于基础题．
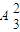=6种方法，利用乘法原理求的结果．解答：解：由题意可得，A中3个元素中只有2个元素的像相同，
从A中3个元素中选出2个元素，使者两个元素的像相同，有c32=3种方法．
再从B中3个元素中找出2和元素作像，有
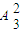=6种方法．根据分步计数原理，这样的映射个数为 3×6=18个，
故选B
点评：本题考查映射的概念，分步计数原理的应用，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目