题目内容
(2012•孝感模拟)已知函数 f(x)=
x2-2alnx+(a-2)x,a∈R.
(Ⅰ)当 a=1 时,求函数 f(x) 的最小值;
(Ⅱ)当 a≤0 时,讨论函数 f(x) 的单调性;
(Ⅲ)是否存在实数a,对任意的 x1,x2∈(0,+∞),且x1≠x2,有
>a,恒成立,若存在求出a的取值范围,若不存在,说明理由.
| 1 |
| 2 |
(Ⅰ)当 a=1 时,求函数 f(x) 的最小值;
(Ⅱ)当 a≤0 时,讨论函数 f(x) 的单调性;
(Ⅲ)是否存在实数a,对任意的 x1,x2∈(0,+∞),且x1≠x2,有
| f(x2)-f(x1) |
| x2-x1 |
分析:(Ⅰ)显然函数f(x)的定义域为(0,+∞),当 a=1 时,求导函数f′(x)=
=
,确定函数的单调性,从而可得f(x)的最小值;
(Ⅱ)∵f′(x)=x-
+(a-2)=
=
,根据 a≤0,将-a与2进行比较,分类讨论,从而可确定函数 f(x) 的单调性;
(Ⅲ)假设存在实数a使得对任意的 x1,x2∈(0,+∞),且x1≠x2,有
>a恒成立,不妨设0<x1<x2,只要
>a,即:f(x2)-ax2>f(x1)-ax1,构建函数(x)=f(x)-ax,只要 g(x)在(0,+∞)为增函数,即使g'(x)≥0在(0,+∞)恒成立,从而可确定是否存在实数a
| x2-x-2 |
| x |
| (x-2)(x+1) |
| x |
(Ⅱ)∵f′(x)=x-
| 2a |
| x |
| x2+(a-2)x-2a |
| x |
| (x-2)(x+a) |
| x |
(Ⅲ)假设存在实数a使得对任意的 x1,x2∈(0,+∞),且x1≠x2,有
| f(x2)-f(x1) |
| x2-x1 |
| f(x2)-f(x1) |
| x2-x1 |
解答:解:(Ⅰ)由题意,函数f(x)的定义域为(0,+∞),…(1分)
当a=1 时,f′(x)=
=
…(2分)
∴当x∈(0,2)时,f′(x)<0,x∈(2,+∞),f'(x)>0.
∴f(x)在x=2时取得极小值且为最小值,其最小值为 f(2)=-2ln2…(4分)
(Ⅱ)∵f′(x)=x-
+(a-2)=
=
,…(5分)
∴(1)当-2<a≤0时,若x∈(0,-a)时,f′(x)>0,f(x)为增函数;
x∈(-a,2)时,f′(x)<0,f(x)为减函数;
x∈(2,+∞)时,f′(x)>0,f(x)为增函数.
(2)当a=-2时,x∈(0,+∞)时,f(x)为增函数;
(3)当a<-2时,x∈(0,2)时,f′(x)>0,f(x)为增函数;
x∈(2,-a)时,f′(x)<0,f(x)为减函数;
x∈(-a,+∞)时,f′(x)>0,f(x)为增函数…(9分)
(Ⅲ)假设存在实数a使得对任意的 x1,x2∈(0,+∞),且x1≠x2,有
>a恒成立,
不妨设0<x1<x2,只要
>a,即:f(x2)-ax2>f(x1)-ax1
令g(x)=f(x)-ax,只要 g(x)在(0,+∞)为增函数
又函数g(x)=
x2-2alnx-2x.
考查函数g′(x)=x-
-2=
=
…(10分)
要使g'(x)≥0在(0,+∞)恒成立,只要-1-2a≥0,即a≤-
,…(12分)
故存在实数a∈(-∞,-
]时,对任意的 x1,x2∈(0,+∞),且x1≠x2,有
>a恒成立,…(14分)
当a=1 时,f′(x)=
| x2-x-2 |
| x |
| (x-2)(x+1) |
| x |
∴当x∈(0,2)时,f′(x)<0,x∈(2,+∞),f'(x)>0.
∴f(x)在x=2时取得极小值且为最小值,其最小值为 f(2)=-2ln2…(4分)
(Ⅱ)∵f′(x)=x-
| 2a |
| x |
| x2+(a-2)x-2a |
| x |
| (x-2)(x+a) |
| x |
∴(1)当-2<a≤0时,若x∈(0,-a)时,f′(x)>0,f(x)为增函数;
x∈(-a,2)时,f′(x)<0,f(x)为减函数;
x∈(2,+∞)时,f′(x)>0,f(x)为增函数.
(2)当a=-2时,x∈(0,+∞)时,f(x)为增函数;
(3)当a<-2时,x∈(0,2)时,f′(x)>0,f(x)为增函数;
x∈(2,-a)时,f′(x)<0,f(x)为减函数;
x∈(-a,+∞)时,f′(x)>0,f(x)为增函数…(9分)
(Ⅲ)假设存在实数a使得对任意的 x1,x2∈(0,+∞),且x1≠x2,有
| f(x2)-f(x1) |
| x2-x1 |
不妨设0<x1<x2,只要
| f(x2)-f(x1) |
| x2-x1 |
令g(x)=f(x)-ax,只要 g(x)在(0,+∞)为增函数
又函数g(x)=
| 1 |
| 2 |
考查函数g′(x)=x-
| 2a |
| x |
| x2-2x-2a |
| x |
| (x-1)2-1-2a |
| x |
要使g'(x)≥0在(0,+∞)恒成立,只要-1-2a≥0,即a≤-
| 1 |
| 2 |
故存在实数a∈(-∞,-
| 1 |
| 2 |
| f(x2)-f(x1) |
| x2-x1 |
点评:本题考查导数知识的运用,考查利用导数确定函数的单调区间,考查是否存在问题,考查分类讨论的数学思想,正确运用好导数工具是关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 (2012•孝感模拟)如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有( )
(2012•孝感模拟)如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有( )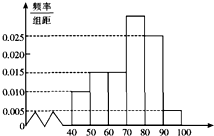 (2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
(2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题: