题目内容
(2012•孝感模拟)某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产1百件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为5百件,产品销售数量为t(百件)时,销售所得的收入为(5t-
t2)万元.
(1)该公司这种产品的年生产量为x百件,生产并销售这种产品所得到的利润关于当年产量x的函数为f(x),求f(x).
(2)当该公司的年产量为多少件时,当年所获得的利润最大.
| 1 | 2 |
(1)该公司这种产品的年生产量为x百件,生产并销售这种产品所得到的利润关于当年产量x的函数为f(x),求f(x).
(2)当该公司的年产量为多少件时,当年所获得的利润最大.
分析:(1)分类讨论:①当0≤x≤5时,②当x>5时,分别写出函数f(x)的表达式,最后利用分段函数的形式写出所求函数解析式即可;
(2)分别求出当0≤x≤5时,及当x>5时,f(x)的最大值,最后综上所述,当x为多少时,f(x)有最大值,即当年产量为多少件时,公司可获得最大年利润.
(2)分别求出当0≤x≤5时,及当x>5时,f(x)的最大值,最后综上所述,当x为多少时,f(x)有最大值,即当年产量为多少件时,公司可获得最大年利润.
解答:解(I)当0<x≤5时,f(x)=5x-
x2-(0.25x+0.5)=-
x2+
-
(2分)
当x>5时,f(x)=25-
×52-(0.25x+0.5)=12-
(4分)
∴f(x)=
(6分)
(2)0≤x≤5时,f(x)=-
(x-
)2+
,
∴在x=
时,f(x)有最大值
万元,(10分)
当x>5时,f(x)=12-
x<12-
×5<
(12分)
综上所述,当x=4.75时,f(x)有最大值,即当年产量为475件时,公司可获得最大年利润(13分)
| 1 |
| 2 |
| 1 |
| 2 |
| 19x |
| 4 |
| 1 |
| 2 |
当x>5时,f(x)=25-
| 1 |
| 2 |
| x |
| 4 |
∴f(x)=
|
(2)0≤x≤5时,f(x)=-
| 1 |
| 2 |
| 19 |
| 4 |
| 345 |
| 32 |
∴在x=
| 19 |
| 4 |
| 345 |
| 32 |
当x>5时,f(x)=12-
| 1 |
| 4 |
| 1 |
| 4 |
| 345 |
| 32 |
综上所述,当x=4.75时,f(x)有最大值,即当年产量为475件时,公司可获得最大年利润(13分)
点评:本题考查了分段函数,以及函数与方程的思想,属于基础题.函数模型为分段函数,求分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值,取各部分的最小者为整个函数的最小值.

练习册系列答案
相关题目
 (2012•孝感模拟)如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有( )
(2012•孝感模拟)如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有( )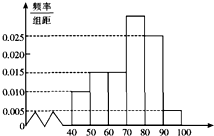 (2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
(2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题: