Question

(本小题满分10分)已知等差数列{a_n}的首项a₁＝1，公差d＞0，且第2项、第5项、第14项分别是一个等比数列的第二项、第三项、第四项．

（Ⅰ）求数列{a_n}的通项公式；

（Ⅱ）设＝（n∈N^*），＝b₁＋b₂＋…＋b_n，是否存在最大的整数t，使得任意的n均有总成立？若存在，求出t；若不存在，请说明理由

 

Answer 1

【答案】

解：（Ⅰ）由题意得（a₁＋d）（a₁＋13d）=（a₁＋4d）²， ……………… 2 分

整理得2a₁d＝d²．

∵a₁＝1，解得（d＝0舍），d＝2．  ………………………………………… 4 分

∴a_n＝2n－1（n∈N^*）．   …………………………………………………… 5 分

（Ⅱ）b_n＝＝＝（－），

∴S_n＝b₁＋b₂＋…＋b_n＝［（1－）＋（－）＋…＋（－）］

＝（1－）＝．   …………………………………… 8 分

假设存在整数t满足S_n＞总成立.

又S_n+1－S_n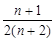＝－＝＞0，

∴数列{S_n}是单调递增的．  

∴S₁＝为S_n的最小值，故＜，即t＜9．

∵t∈N^*，

∴适合条件的t的最大值为8．   ……………………………… 10分

 

【解析】略