题目内容
已知实数a满足1<a≤2,设函数f (x)=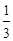 x3-
x3-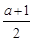 x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=4x3+3bx2-6(b+2)x (b∈R) 的极小值点与f (x)的极小值点相同,
求证:g(x)的极大值小于等于10.
【答案】
(Ⅰ)解:f (x)的极小值为f (2)=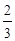 .
.
(Ⅱ) 略
【解析】在高中阶段,导数是研究函数性质的重要而有效的工具之一,包括函数的单调性,极值,最值等,本题就是利用导函数研究函数的极值.近两年的高考题中,对导数部分的考查是越来越常见,其重要性也不言而喻
(Ⅰ)将a=2代入到解析式中,并求导.令f′(x)=0,求出极值点,并列表判断极大值极小值点.
(Ⅱ)一方面,利用(Ⅰ)的结论,找出f(x)的极小值点a,即为g(x)的极小值点.另一方面,对g(x)求导,求出极小值点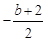 .再建立等式,即
.再建立等式,即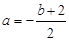 ,得到a,b的关系式.由a的范围算出极大值g(1)的范围,从而得证.
,得到a,b的关系式.由a的范围算出极大值g(1)的范围,从而得证.

练习册系列答案
相关题目