题目内容
【题目】如图,过点E(1,0)的直线与圆O:x2+y2=4相交于A、B两点,过点C(2,0)且与AB垂直的直线与圆O的另一交点为D. 
(1)当点B坐标为(0,﹣2)时,求直线CD的方程;
(2)求四边形ABCD面积S的最大值.
【答案】
(1)解:当B(0,﹣2)时,直线AB的斜率为 ![]() ,
,
∵CD与AB垂直,∴直线CD的斜率为﹣ ![]() ,
,
∴直线CD的方程为y=﹣ ![]() (x﹣2),即x+2y﹣2=0.
(x﹣2),即x+2y﹣2=0.
(2)解:当直线AB与x轴垂直时,AB=2 ![]() ,CD=4,
,CD=4,
∴四边形ACBD的面积S= ![]() ,
,
当直线AB与x轴不垂直时,设直线AB方程为y=k(x﹣1),
即kx﹣y﹣k=0,
则直线CD方程为y=﹣ ![]() ,即x+ky﹣2=0,
,即x+ky﹣2=0,
点O到直线AB的距离为 ![]() ,
,
∴AB=2 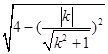 =2
=2 ![]() ,
,
CD=2  =4
=4 ![]() ,
,
则四边形ACBD面积S= ![]() =
= ![]() =4
=4  ,
,
令k2+1=t>1(当k=0时,四边形ACBD不存在),
∴  =4
=4 ![]() ∈(0,4
∈(0,4 ![]() ),
),
∴四边形ABCD面积S的最大值为4 ![]() .
.
【解析】(1)当B(0,﹣2)时,直线AB的斜率为2,由CD与AB垂直,直线CD的斜率为﹣ ![]() ,由此能求出直线CD的方程.(2)当直线AB与x轴垂直时,AB=2
,由此能求出直线CD的方程.(2)当直线AB与x轴垂直时,AB=2 ![]() ,CD=4,四边形ACBD的面积,当直线AB与x轴不垂直时,设直线AB方程为kx﹣y﹣k=0,则直线CD方程为x+ky﹣2=0,求出点O到直线AB的距离,从而得到弦长AB和CD,由此利用配方法能求出四边形ACBD面积的最大值.
,CD=4,四边形ACBD的面积,当直线AB与x轴不垂直时,设直线AB方程为kx﹣y﹣k=0,则直线CD方程为x+ky﹣2=0,求出点O到直线AB的距离,从而得到弦长AB和CD,由此利用配方法能求出四边形ACBD面积的最大值.
【考点精析】认真审题,首先需要了解直线与圆的三种位置关系(直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点).

 名校课堂系列答案
名校课堂系列答案【题目】国家实施二孩放开政策后,为了了解人们对此政策持支持态度是否与年龄有关,计生部门将已婚且育有一孩的居民分成中老年组(45岁以上,含45岁)和中青年组(45岁以下,不含45岁)两个组别,每组各随机调查了50人,对各组中持支持态度和不支持态度的人所占的频率绘制成等高条形图,如图所示: 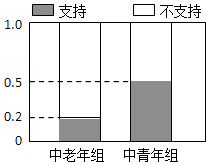
支持 | 不支持 | 合计 | |
中老年组 | 50 | ||
中青年组 | 50 | ||
合 计 | 100 |
(1)根据以上信息完成2×2列联表;
(2)是否有99%以上的把握认为人们对此政策持支持态度与年龄有关?
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
附: ![]() .
.