题目内容
四棱锥S-ABCD的各棱长都相等,E是侧棱SA的中点,则BE与底面ABCD所成角的正弦值是 .
分析:过S作SO⊥平面ABCD,由四棱锥S-ABCD的各棱长都相等,可得底面ABCD为正方形,建立空间直角坐标系求出平面ABCD的法向量和BE的坐标表示,利用向量数量积公式求BE与底面ABCD所成角的正弦值.
解答:解:过S作SO⊥平面ABCD,∵四棱锥S-ABCD的各棱长都相等,
∴底面ABCD为菱形,又OA=OB=OC=OD,∴底面ABCD为正方形,
设棱长为1,建立空间直角坐标系如图:
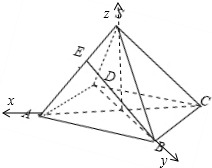
则S(0,0,
),O(0,0,0),B(0,
,0),A(
,0,0),E(
,0,
),
=(
,-
,
),
=(0,0,
),
∵
为平面ABCD的法向量,cos<
,
>=
=
,
∴BE与底面ABCD所成角的正弦值是
.
故答案是
.
∴底面ABCD为菱形,又OA=OB=OC=OD,∴底面ABCD为正方形,
设棱长为1,建立空间直角坐标系如图:

则S(0,0,
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
| BE |
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
| OS |
| ||
| 2 |
∵
| OS |
| BE |
| OS |
| ||||||||
|
| ||
| 6 |
∴BE与底面ABCD所成角的正弦值是
| ||
| 6 |
故答案是
| ||
| 6 |
点评:本题采用了向量坐标运算求线面角,解答的关键是建立空间直角坐标系,求得平面的法向量与直线的方向向量.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
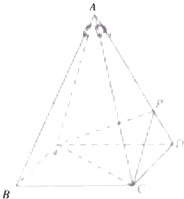 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的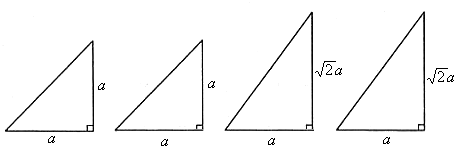
 (2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示.
(2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示. 如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=
如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=