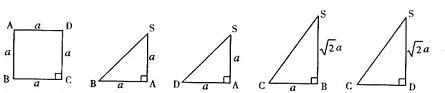
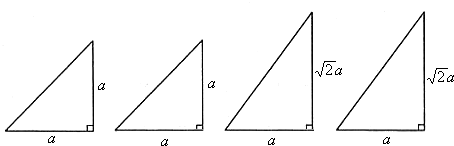
题目内容
下面的一组图形为侧棱SA垂直于底面ABCD的某一四棱锥S-ABCD的侧面与底面,画出四棱锥S-ABCD的空间图形并研究
(I)求直线SC与平面SAD所成的角的大小;
(Ⅱ)求二面角B-SC-D的大小;
(Ⅲ)求此四棱锥S-ABCD外接球半径与内切球半径之和.
(I)求直线SC与平面SAD所成的角的大小;
(Ⅱ)求二面角B-SC-D的大小;
(Ⅲ)求此四棱锥S-ABCD外接球半径与内切球半径之和.

分析:(I)证明∠DSC为直线SC与平面SAD所成的角,利用正切函数,可得结论;
(II)作BE⊥SC,垂足为E,连接DE,则DE⊥SC,可得∠BED为二面角B-SC-D的平面角,利用余弦定理可求;
(III)SC为S-ABCD外接于球的直径,利用等体积法,可求内切球半径,从而可得结论.
(II)作BE⊥SC,垂足为E,连接DE,则DE⊥SC,可得∠BED为二面角B-SC-D的平面角,利用余弦定理可求;
(III)SC为S-ABCD外接于球的直径,利用等体积法,可求内切球半径,从而可得结论.
解答: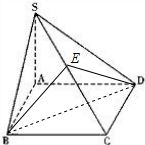 解:(I)如图所示,由题意,SA=AB=a,SA⊥AB,SA⊥AD,且AB、AD是面ABCD内的交线,∴SA⊥底面ABCDSA⊥平面ABCD,底面ABCD是矩形,
解:(I)如图所示,由题意,SA=AB=a,SA⊥AB,SA⊥AD,且AB、AD是面ABCD内的交线,∴SA⊥底面ABCDSA⊥平面ABCD,底面ABCD是矩形,
则CD⊥平面SAD,∴∠DSC为直线SC与平面SAD所成的角,
∵CD=a,SD=
a
∴tan∠DSC=
∴直线SC与平面SAD所成的角为arctan
;
(II)作BE⊥SC,垂足为E,连接DE,则DE⊥SC,
∴∠BED为二面角B-SC-D的平面角
∵BC=a,SB=
a,∴SC=
a
∴BE=
=
a
在△BED中,cos∠BED=
=-
∴∠BED=120°;
(III)SC为S-ABCD外接于球的直径,SC=
a,∴半径为
a
设内切球半径为r,则
•(
a2×2+
a•
a×2)r=
×a2×a
∴r=(
-1)a
∴四棱锥S-ABCD外接球半径与内切球半径之和为
a+(
-1)a.
 解:(I)如图所示,由题意,SA=AB=a,SA⊥AB,SA⊥AD,且AB、AD是面ABCD内的交线,∴SA⊥底面ABCDSA⊥平面ABCD,底面ABCD是矩形,
解:(I)如图所示,由题意,SA=AB=a,SA⊥AB,SA⊥AD,且AB、AD是面ABCD内的交线,∴SA⊥底面ABCDSA⊥平面ABCD,底面ABCD是矩形,则CD⊥平面SAD,∴∠DSC为直线SC与平面SAD所成的角,
∵CD=a,SD=
| 2 |
∴tan∠DSC=
| ||
| 2 |
∴直线SC与平面SAD所成的角为arctan
| ||
| 2 |
(II)作BE⊥SC,垂足为E,连接DE,则DE⊥SC,
∴∠BED为二面角B-SC-D的平面角
∵BC=a,SB=
| 2 |
| 3 |
∴BE=
a•
| ||
|
| ||
| 3 |
在△BED中,cos∠BED=
(
| ||||||||
2•
|
| 1 |
| 2 |
∴∠BED=120°;
(III)SC为S-ABCD外接于球的直径,SC=
| 3 |
| ||
| 2 |
设内切球半径为r,则
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
∴r=(
| 2 |
∴四棱锥S-ABCD外接球半径与内切球半径之和为
| ||
| 2 |
| 2 |
点评:本题考查线面角,面面角,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目