题目内容
等比数列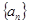 的前n项和
的前n项和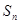 ,已知对任意的
,已知对任意的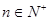 ,点
,点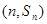 均在函数
均在函数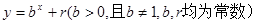 的图像上.
的图像上.
(1)求r的值.
(2)当b=2时,记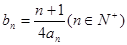 ,求数列
,求数列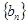 的前n项和
的前n项和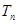 .
.
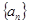 的前n项和
的前n项和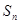 ,已知对任意的
,已知对任意的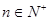 ,点
,点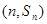 均在函数
均在函数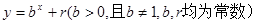 的图像上.
的图像上.(1)求r的值.
(2)当b=2时,记
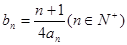 ,求数列
,求数列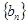 的前n项和
的前n项和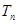 .
.(1)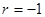 ;(2)
;(2)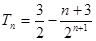 .
.
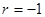 ;(2)
;(2)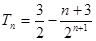 .
.试题分析:(1)将点
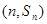 代入
代入 均为常数),当
均为常数),当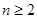 时,
时,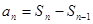 ;当
;当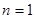 时,
时,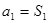 ,检验
,检验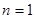 是否满足
是否满足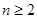 时情形,由数列
时情形,由数列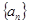 是等比数列,则
是等比数列,则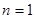 满足
满足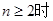 的情形,可列方程求
的情形,可列方程求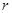 ;(2)要求数列的前
;(2)要求数列的前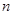 项和,先考虑其通项公式,由(1)知数列
项和,先考虑其通项公式,由(1)知数列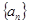 的通项公式,代入
的通项公式,代入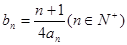 ,可求数列
,可求数列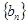 的通项公式,再根据通项公式的类型,求前项
的通项公式,再根据通项公式的类型,求前项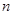 项和
项和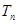 .
.试题解析:(1)因为对任意的
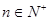 ,点
,点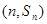 均在函数
均在函数 均为常数)所以可得
均为常数)所以可得 ,
,当
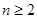 时,
时,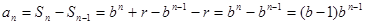 ,
,当
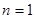 时,
时,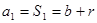 ,
,因为数列
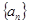 是等比数列,所以
是等比数列,所以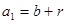 满足
满足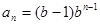 ,所以
,所以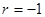 ,
,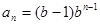 .
.(2)当
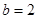 时,
时,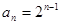 ,
,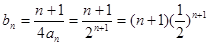
则
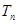 =
=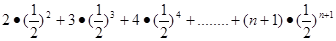
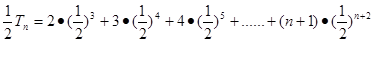
两式相减可得
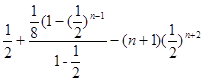
所以,
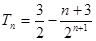 .
. 项和与项的关系;2、错位相减法.
项和与项的关系;2、错位相减法.
练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 ,数列
,数列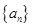 满足
满足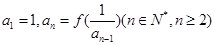 .
.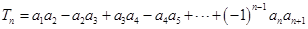 ,若
,若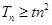 对
对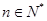 恒成立,求实数
恒成立,求实数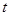 的取值范围;
的取值范围;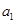 为首项,公比为
为首项,公比为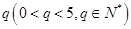 的数列
的数列 ,
,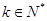 ,使得数列
,使得数列 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.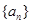 的前
的前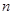 项和为
项和为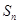 ,公差
,公差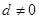 ,且
,且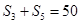 ,
,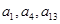 成等比数列.
成等比数列.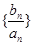 是首项为1公比为3 的等比数列,求数列
是首项为1公比为3 的等比数列,求数列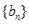 前
前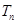 .
.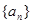 的前n项和为
的前n项和为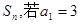 ,
,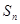 和
和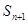 满足等式
满足等式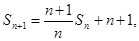
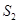 的值;
的值;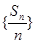 是等差数列;
是等差数列;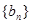 满足
满足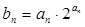 ,求数列
,求数列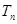 ;
;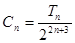 ,求证:
,求证: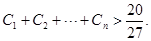
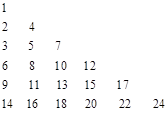
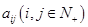 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第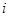 行、从左往右数第
行、从左往右数第 个数,如
个数,如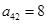 .若
.若 ,则
,则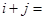 .
.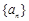 中,若
中,若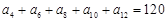 ,则
,则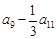 的值为 .
的值为 .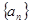 满足
满足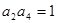 ,
,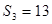 ,
,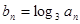 ,则数列
,则数列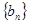 的前10项和是( ).
的前10项和是( ).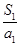 ,
,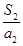 ,…,
,…,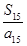 中最大的是( )
中最大的是( )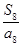
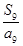
 中,
中,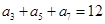 ,那么
,那么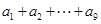 的值为 .
的值为 .