题目内容
(本题满分13分)本题共有2个小题,第1小题满分6分,第2小题满分7分.
已知椭圆![]() :
:![]() (
(![]() )过点
)过点![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,且
,且
![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是直线
是直线![]() 上的两个动点,且
上的两个动点,且![]() ,则以
,则以![]() 为直径的圆
为直径的圆![]() 是否过定点?请说明理由.
是否过定点?请说明理由.
解:(1)设点![]() 的坐标分别为
的坐标分别为![]() ,
,
则![]()
故![]() ,可得
,可得![]() , …………………2分
, …………………2分
所以![]() ,…………………4分
,…………………4分
故![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() . ……………………………6分
. ……………………………6分
(2)设![]() 的坐标分别为
的坐标分别为![]() ,则
,则![]() ,
,
又![]() ,可得
,可得![]() ,即
,即![]() , …………………8分
, …………………8分
又圆![]() 的圆心为
的圆心为![]() 半径为
半径为![]() ,
,
故圆![]() 的方程为
的方程为![]() ,
,
即![]() ,
,
也就是![]() , ……………………11分
, ……………………11分
令![]() ,可得
,可得![]() 或2,
或2,
故圆![]() 必过定点
必过定点![]() 和
和![]() . ……………………13分
. ……………………13分
(另法:(1)中也可以直接将点![]() 坐标代入椭圆方程来进行求解;(2)中可利用圆C直径的两端点直接写出圆
坐标代入椭圆方程来进行求解;(2)中可利用圆C直径的两端点直接写出圆![]() 的方程)
的方程)

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
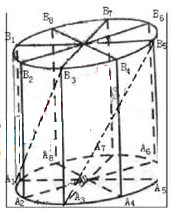 (1)当圆柱底面半径
(1)当圆柱底面半径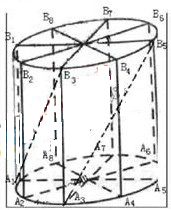 (1)当圆柱底面半径
(1)当圆柱底面半径 满足
满足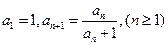 ,数列
,数列 满足
满足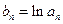 ,数列
,数列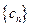
 .
. ,
,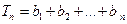 ,试比较
,试比较 与
与 的大小,并证明;
的大小,并证明;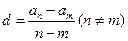 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列 不是一个常数,但
不是一个常数,但 呢,若会,请求出
呢,若会,请求出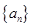 满足
满足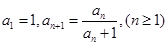 ,数列
,数列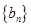 满足
满足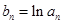 ,数列
,数列
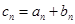 .
. ,
,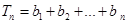 ,试比较
,试比较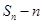 与
与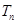 的大小,并证明;
的大小,并证明;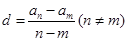 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列 不是一个常数,但
不是一个常数,但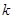 呢,若会,请求出
呢,若会,请求出