已知椭圆C:$\frac{x^2}{16}+\frac{y^2}{12}=1$.点M与C的焦点不重合.若M关于C的两焦点的对称点分别为P.Q.线段MN的中点在C上.则|PN|+|QN|=16．题目和参考答案——青夏教育精英家教网——

题目内容

3．已知椭圆C：$\frac{x^2}{16}+\frac{y^2}{12}=1$，点M与C的焦点不重合，若M关于C的两焦点的对称点分别为P，Q，线段MN的中点在C上，则|PN|+|QN|=16．

分析先作出图形，由椭圆方程，得a的值，设F₁，F₂分别是椭圆C的左、右焦点，K为线段MN的中点，易得KF₁，KF₂分别是△NBM和△NAM的中位线，可得|NB|与|KF₁|，及|NA|与|KF₂|的数量关系，再利用椭圆的定义，即可达到目的．

解答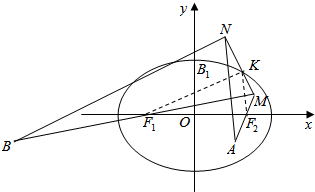解：设椭圆C的长轴长为2a，则由$\frac{x^2}{16}+\frac{y^2}{12}=1$，得a=4，
又设F₁，F₂分别是椭圆C的左、右焦点，K为线段MN的中点，
如右图所示，由已知条件，易得F₁，F₂分别是线段MB，MA的中点，
则在△NBM和△NAM中，有|NB|=2|KF₁|，|NA|=2|KF₂|，
又由椭圆定义，得|KF₁|+|KF₂|=2a=8，
故|AN|+|BN|=2（|KF₁|+|KF₂|）=16．
故答案为：16．

点评本题主要考查了椭圆定义的运用，三角形中位线的性质等．本题涉及的动点较多，解题的突破口是作出图形，根据图形的几何特征，寻找两个三角形的中位线，关键是利用椭圆的定义，抓住变化中确定的数量关系．

练习册系列答案

课外作业系列答案

综合复习与测试系列答案

课时总动员系列答案

期末赢家系列答案

天天向上提分金卷系列答案

新思路辅导与训练系列答案

说明与检测系列答案

全程优选测试卷系列答案

沸腾英语系列答案

考点同步解读系列答案

相关题目

11．函数f（x）=$\sqrt{4-|x|}$+lg$\frac{{{x^2}-5x+6}}{x-3}$的定义域为（　　）

（2，3）∪（3，4]

（-1，3）∪（3，6]

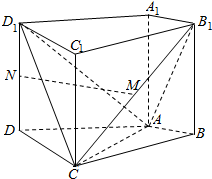如图，在四棱柱ABCD-A₁B₁C₁D₁中，侧棱AA₁⊥底面ABCD，AB⊥AC，AB=1，AC=AA₁=2，AD=CD=$\sqrt{5}$，且点M和N分别为B₁C和D₁D的中点．
（Ⅰ）求证：MN∥平面ABCD
（Ⅱ）求二面角D₁-AC-B₁的正弦值；
（Ⅲ）设E为棱A₁B₁上的点，若直线NE和平面ABCD所成角的正弦值为$\frac{1}{3}$，求线段A₁E的长．

9．已知数列{a_n}满足a₁=$\frac{1}{2}$且a_n+1=a_n-a_n²（n∈N^*）
（1）证明：1＜$\frac{a_n}{{{a_{n+1}}}}$≤2（n∈N^*）；
（2）设数列{a_n²}的前n项和为S_n，证明$\frac{1}{2（n+2）}≤\frac{S_n}{n}≤\frac{1}{2（n+1）}$（n∈N^*）．

16．在直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}{x=3+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$（t为参数），以原点为极点，x轴正半轴为极轴建立极坐标系，⊙C的极坐标方程为ρ=2$\sqrt{3}$sinθ．
（Ⅰ）写出⊙C的直角坐标方程；
（Ⅱ）P为直线l上一动点，当P到圆心C的距离最小时，求P的直角坐标．

8．在平面直角坐标系xOy中，圆O：x²+y²=1，P为直线l：x=t（1＜t＜2）上一点．
（1）已知t=$\frac{4}{3}$．
①若点P在第一象限，且OP=$\frac{5}{3}$，求过点P的圆O的切线方程；
②若存在过点P的直线交圆O于点A，B，且B恰为线段AP的中点，求点P纵坐标的取值范围；
（2）设直线l与x轴交于点M，线段OM的中点为Q，R为圆O上一点，且RM=1，直线RM与圆O交于另一点N，求线段NQ长的最小值．

15．设函数f（x）=ln（x+1）+a（x²-x），其中a∈R，
（Ⅰ）讨论函数f（x）极值点的个数，并说明理由；
（Ⅱ）若?x＞0，f（x）≥0成立，求a的取值范围．

12．已知函数f（x）=ln$\frac{1+x}{1-x}$，
（Ⅰ）求曲线y=f（x）在点（0，f（0））处的切线方程；
（Ⅱ）求证，当x∈（0，1）时，f（x）＞$2（x+\frac{{x}^{3}}{3}）$；
（Ⅲ）设实数k使得f（x）$＞k（x+\frac{{x}^{3}}{3}）$对x∈（0，1）恒成立，求k的最大值．

13．已知${\overrightarrow e_1}，{\overrightarrow e_2}$是空间单位向量，${\overrightarrow e_1}•{\overrightarrow e_2}=\frac{1}{2}$，若空间向量$\overrightarrow b$满足$\overrightarrow b•{\overrightarrow e_1}=2，\overrightarrow b•{\overrightarrow e_2}=\frac{5}{2}$，且对于任意x，y∈R，$|{\overrightarrow b-（x\overrightarrow{e_1}+y\overrightarrow{e_2}）}|≥|{\overrightarrow b-（{x_0}\overrightarrow{e_1}+{y_0}\overrightarrow{e_2}）}|$=1（x₀，y₀∈R），则x₀=1，y₀=2，$|{\overrightarrow b}$|=2$\sqrt{2}$．