Question

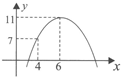某汽车运输公司购买了-批豪华大客车投入客运，据市场分析，每辆客车营运的总利润y（万元）与营运年数x（x∈N^*）为二次函数关系，如图所示，则每辆客车营运多少年使其营运年平均利润最大（　　）

A．3

B．4

C．5

D．6

Answer 1

分析：由题图可得营运总利润y=-a（x-6）²+11，把（4，7）代入可得a，解得a=1．可得表达式．可得营运的年平均利润

y

x

，利用基本不等式即可得出．

解答：解：由题图可得营运总利润y=-a（x-6）²+11，把（4，7）代入可得7=-a（4-6）²+11，解得a=1．
∴y=-（x-6）²+11．
则营运的年平均利润

y

x

=-x-

25

x

+12．
∵x∈N^*，∴

y

x

≤-2

x• 25 x

+12=2，当且仅当x=5时取等号．
∴x=5时营运的平均利润最大．
故选C．

点评：本题考查了二次函数的图象与性质、基本不等式的性质，属于基础题．