题目内容
(本小题满分12分)
某班t名学生在2011年某次数学测试中,成绩全部介于80分与130分之间,将测试结果按如下方式分成五组,第一组[80,90);第二组[90,100)…第五组
[120,130],下表是按上述分组方法得到的频率分布表:
|
分组 |
频数 |
频率 |
|
[80,90) |
x |
0.04 |
|
[90,100) |
9 |
y |
|
[100,110) |
z |
0.38 |
|
[110,120) |
17 |
0.34 |
|
[120,130] |
3 |
0.06 |
(Ⅰ) 求t及分布表中x,y,z的值;
(Ⅱ)设m,n是从第一组或第五组中任意抽取的两名学生的数学测试成绩,求事件
“|m—n|≤10”的概率.
【答案】
解:(Ⅰ)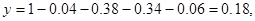 ……2分
……2分
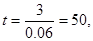 ……3分
……3分 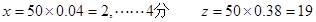 …5分
…5分
(II)第一组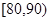 中有2个学生,数学测试成绩设为
中有2个学生,数学测试成绩设为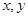
第五组[120,130]中有3个学生,数学测试成绩设为A、B、C……1分
则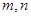 可能结果为
可能结果为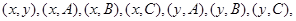 ,
,
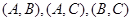 共10种
………4分
共10种
………4分
使|m—n|≤10成立有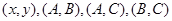 4种…………6分
4种…………6分
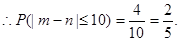 即事件
即事件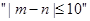 的概率为
的概率为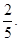 ………7分
………7分
【解析】略

练习册系列答案
相关题目