题目内容
【题目】已知四棱柱![]() 的所有棱长都为2,且
的所有棱长都为2,且![]() .
.
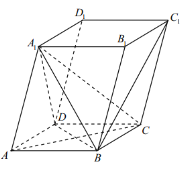
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 的正弦值.
的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)要证平面![]() 平面
平面![]() ,转化为证明
,转化为证明![]() 平面
平面![]() ,通过证明
,通过证明![]() 及
及![]() 可得;
可得;
(2)连接![]() ,由(1)可得
,由(1)可得![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角
所成的角![]() ,在
,在![]() 中求角
中求角![]() 的正弦值.另外可以用向量法求线面角.
的正弦值.另外可以用向量法求线面角.
(1)证明:设![]() 与
与![]() 的交点为
的交点为![]() ,连接
,连接![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
又因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
另由![]() 且
且![]() ,
,
所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
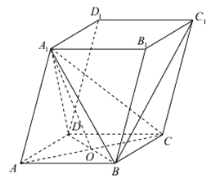
(2)(法一)连接![]() ,由(1)知
,由(1)知![]() 平面
平面![]() ,
,
所以![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角
所成的角![]() ,
,
在菱形![]() 中,
中,![]() ,
,
故![]() ,
,
所以![]()
又因为![]() ,所以
,所以![]() ,
,
所以![]() .
.
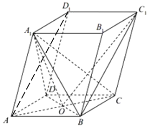
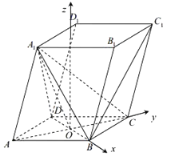
(法二)过![]() 作直线
作直线![]() 平面
平面![]() ,分别以
,分别以![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 轴,建立如图所示空间直角坐标系,
轴,建立如图所示空间直角坐标系,
依题意,得![]() ,
,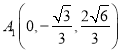 ,
,![]() ,
,![]() ,
,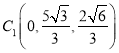 ,
,
所以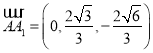 ,
,![]() ,
,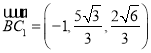 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
所以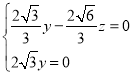 ,令
,令![]() ,则
,则![]() ,即
,即![]() ,
,
所以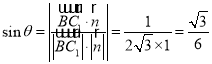 ,
,
即直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 的正弦值为
的正弦值为![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】小军的微信朋友圈参与了“微信运动”,他随机选取了40位微信好友(女20人,男20人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
5860 8520 7326 6798 7325 8430 3216 7453 11754 9860
8753 6450 7290 4850 10223 9763 7988 9176 6421 5980
男性好友走路的步数情况可分为五个类别(说明:m~n表示大于等于m,小于等于n):A(0~2000步)1人,B(2001~5000步)2人,C(5001~8000步)3人,D(8001~10000步)6人,E(10001步及以上)8人.若某人一天的走路步数超过8000步被系统认定为“健康型”,否则被系统认定为“进步型”.
(1)请根据选取的样本数据完成下面的![]() 列联表,并根据此判断能否有95%以上的把握认为“认定类型”与“性别”有关?
列联表,并根据此判断能否有95%以上的把握认为“认定类型”与“性别”有关?
健康型 | 进步型 | 总计 | |
男 | 20 | ||
女 | 20 | ||
总计 | 40 |
(2)从小军的40位好友中该天走路步数不超过5000的中随机抽取3人,若![]() 表示抽到的三人分别是x,y,z,试用该表示法列举出试验所有可能的结果.若记“恰好抽到了一位女性好友”为事件A,求事件A的概率.
表示抽到的三人分别是x,y,z,试用该表示法列举出试验所有可能的结果.若记“恰好抽到了一位女性好友”为事件A,求事件A的概率.
附: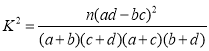 ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(AQI)的检测数据,结果统计如表:
AQI |
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 重度污染 |
天数 | 6 | 14 | 18 | 27 | 25 | 10 |
(1)从空气质量指数属于[0,50],(50,100]的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
(2)已知某企业每天因空气质量造成的经济损失y(单位:元)与空气质量指数x的关系式为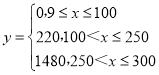 ,假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为
,假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为![]() .9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
.9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
(i)记该企业9月每天因空气质量造成的经济损失为X元,求X的分布列;
(ii)试问该企业7月、8月、9月这三个月因空气质量造成的经济损失总额的数学期望是否会超过2.88万元?说明你的理由.

